Tác động của Tiến động và Chương động đến vị trí thiên thể trên bầu trời
Tiến động Mặt Trăng – Mặt Trời
Hiện tượng tiến động được phát hiện bởi Hipparchus (192TCN – 120TCN) vào năm 127 TCN thông qua những quan sát của ông qua gần một phần tư thế kỷ, ông đã đưa ra kết luận: kinh độ của ngôi sao hiện ra và thay đổi với tốc độ 36” mỗi năm (thực tế khoảng 50”) trong khi vĩ độ không có sự biến đổi. Hiện tượng này được giải thích theo một trong hai cách: 1, tất cả các ngôi sao được quan sát cùng chuyển động trên đường kinh tuyến- giả thiết này không thể xảy ra; 2, về cơ bản nó liên quan đến một điểm- điểm xuân phân Ƴ (mốc xác định kinh độ hoàng đạo). Ta có Ƴ là một trong hai giao điểm của đường xích đạo và đường hoàng đạo trên thiên cầu; các quan sát cho thấy, không có sự thay đổi trong vĩ độ của ngôi sao, do đó, đường hoàng đạo là cố định. Theo giả thiết thứ hai này, đã làm sáng rõ được kết luận của Hipparchus, nó cho thấy đường xích đạo và đương nhiên là cả điểm xuân phân nữa chuyển động làm cho kinh độ của ngôi sao biến đổi đôi chút khi quan sát.
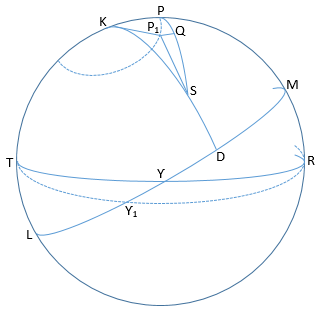Trong hình vẽ bên, LƳM là đường hoàng đạo cố định,, LƳR làđường xích đạo tại thời điểm t và LƳ1R là đường xích đạo một năm sau đó. Trong một năm điểm xuân phân di chuyển từ Ƴ tới Ƴ1 và do đó, kinh độ của ngôi sao tăng ƳD tới Ƴ1D (khoảng 50”). Chuyển động dọc theo đường hoàng đạo của điểm xuân phân được gọi là tiến động của điểm phân. Từ đây, kết luận của Hipparchus được thỏa mãn thông qua việc điểm xuân phân di chuyển chậm, từ đó dẫn đến sự thay đổi của đường xích đạo trời. Do đó, cực P di chuyển đến P1 quanh K trong một vòng tròn nhỏ. Góc cung KP hoặc KP1 cho bởi độ nghiêng ε và KP nằm trên vòng tròn lớn vuông góc với vòng tròn lớn đi qua KƳ và vòng tròn lớn KP1 vuông góc với vòng tròn lớn đi qua KƳ1. Do đó, góc cầu PKP1 bằng số đo cung ƳƳ1.
Ở trên, ta đã nói đến việc cực P di chuyển trên một vòng tròn nhỏ quanh K với chu kỳ 25.920 năm (chu kỳ Platon). Tại thời điểm này thiên cực Bắc gần ngôi sao Polaris (sao Bắc Cực), trong suốt chu kỳ di chuyển của nó sắp tới, nó sẽ lần lượt dịch chuyển qua các ngôi sao Deneb (Thiên Tân), Vega (Chức Nữ) và Alpha Thiên Long.
Newton là người đầu tiên giải thích chính xác theo thuyết động lực của tiến động. Ta hãy quan sát một hiện tượng khá quen thuộc là cù quay khi nó quay quanh trục OC nghiêng một góc i so với trục đứng OD và điểm D nằm trên mặt bàn cố định.
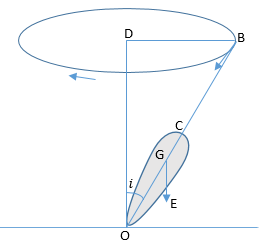Nếu G là trọng tâm của cù quay, trọng lực của nó là GE nghiêng một góc i so với chiều thắng đứng và dường như nó sẽ đem lại một kết quả là cù quay sẽ tiếp xúc với mặt bàn. Nhưng do ngoài chuyển động quay quanh trục OC, nó còn có them một chuyển động khác nữa là trục OC chuyển động xuay quanh trục thẳng đứng. Khi ta nhìn vào điểm B, ta sẽ nhìn thấy nó chuyển động trên một đường tròn xung quanh điểm D nằm trên trục đứng OD và trục OC tạo nên một hình nón trên mặt bàn và hướng chuyển động của trục OC vuông góc với mặt phẳng chứa OC và OD. Chuyển động này được gọi là tiến động.
Bây giờ chuyển sang xem xét chuyển động của trục Trái Đất dưới tác động của Mặt Trăng – Mặt Trời. Nếu Trái Đất có dạng hình cầu, mật độ vật chất của bất kỳ điểm nào phụ thuộc vào khoảng cách của nó tới tâm; do đó, lực hút của Mặt Trăng và Mặt Trời đều đi qua tâm của Trái Đất và do đó, không gây ra chuyển động thay đổi hướng của trục quay. Nhưng hình dạng của Trái Đất không phải là hình cầu với đường xích đạo nằm trên một mặt phẳng cơ bản và Mặt Trời và Mặt Trăng không nằm trên mặt phẳng cơ bản, ngoại trừ hai trường hợp trong suốt chu kỳ quỹ đạo khi xích vĩ bằng 0o; hướng của lực hấp dẫn Mặt Trăng và Mặt Trời do đó không đi qua tâm của Trái Đất, do đó, nó sẽ tồn tại một momen lực ở tâm Trái Đất. Xem xét đối với Mặt Trời, momen lực của Mặt Trời làm cho Mặt phẳng xích đạo Trái Đất có xu hướng chuyển động về đồng phẳng với mặt phẳng hoàng đạo, như trong trường hợp vừa chỉ ra cho con quay, momen trọng lực của cù quay tại điểm O làm cho trục OC có xu hướng tiếp cận với mặt bàn. Các kết quả động lực học cho Trái Đất tương tự cho cù quay; trục của Trái Đất, trong bất kỳ thời điểm nào, chuyển động theo hướng vuông góc với mặt phẳng chứa trục và Mặt Trời; cùng với nó, nó còn có thêm một chuyển động hình nón theo hướng cực hoàng đạo và điểm phân di chuyển ngược hướng dọc theo đường hoàng đạo theo hướng ƳƳ1. Tác động cơ bản của Mặt Trăng lên hướng của trục Trái Đất cũng tương tự. Kết hợp tạo nên chuyển động ngược chiều của điểm xuân phân trên đường hoàng đạo theo hướng ƳƳ1 gọi là tiến động Mặt Trăng – Mặt Trời, khoảng 2/3 thành phần của tiến động gây ra bởi Mặt Trăng và phần còn lại gây ra bởi Mặt Trời. Một số tác động có tính chất chu kỳ được loại khỏi tiến động Mặt Trăng – Mặt Trời.
Cho ψ là tiến động Mặt Trăng – Mặt Trời trong một năm. Ta có 
. Nếu (α,δ) và (α1,δ1) là tọa độ của ngôi sao S xét trong đường hoàng đạo TƳR và TƳ1R. Ta có: PS = 90o – δ; P1S = 90o – δ1; KPS = 90o + α; KP1S = 90o + α1; KS = 90o – β; PKS = 90o – λ và P1KS = 90o – λ1 với β là vĩ độ của ngôi sao và λ, λ1 là kinh độ tương ứng của ngôi sao so với Ƴ và Ƴ1. Ta cũng có KP = KP1 = ε. Đặt Δα = α1 – α và Δδ = δ1 – δ. Sử dụng 3 công thức đầu cho tam giác cầu KPS, ta có:
sin δ = cos ε.sin β + sin ε.cos β.sin λ
Lấy vi phân: cos δ.Δδ = sin ε.cos β.cos λ.Δλ
cos α.cos δ = cos β.cos λ
Lấy vi phân: sin α.cos δ.Δα + cos α.sin δ.Δδ = Δλ.cos β.sin λ
cos β.sin λ = sin δ. sin ε + cos δ.cos ε.sin α
Kết hợp các phương trình lại ta có:
Δδ = Δλ.sin ε.cos α
sin α.cos δ.Δα = Δλ.(cos β.sin λ – sin ε. cos2 α. sin δ)
Δα = Δλ.(cos ε + sin ε. sin α.tan δ)
Mà ta lại có: ψ = Δλ nên:
Δα = ψ.(cos ε + sin ε. sin α.tan δ)
Δδ = ψ.sin ε.cos α
Chương động
Giá trị của ψ ở các công thức trên biểu thị cho sự thay đổi của điểm xuân phân trong kinh độ trong một năm và dường như nó không đổi (khoảng 50” mỗi năm), nơi vòng quay của điểm phân trên đường hoàng đạo với chu kỳ 25.920 năm. Nó sẽ là một hằng số nếu kinh độ của Mặt Trăng và Mặt Trời cố định bằng 0, thì lực hấp dẫn của mỗi lực lên phỏng cầu Trái Đất sẽ không đổi và như nhau qua tâm Trái Đất.
Trước tiên xem xét vị trí của Mặt Trời trên đường hoàng đạo. Trong mối quan hệ chặt chẽ với độ nghiêng của Trái Đất tạo một góc thay đổi b.(1 – sin 2ʘ) với b là một hằng số. Kinh độ thay đổi theo t năm là a1.t + l.sin (2ʘ) với ʘ là kinh độ Mặt Trời và a1, l là những hằng số đúng theo thuyết động lực học. Trong đó a1.t cho biết sự thay đổi và hình thức chuyển động của ψ trên đường hoàng đạo và cách thức chuyển động thông thường, những trường không đổi đặc biệt này được gọi là trường tiến động, còn l.sin (2ʘ) gọi là chu kỳ riêng. Nó bằng 0 nếu kinh độ Mặt Trời là k.90o. Nếu t2 là điểm phân lúc a1.t thì Ƴ3 là điểm phân cho bởi a1.t + l.sin (2ʘ). Nói một cách dễ hiểu, khoảng cách Ƴ2 và Ƴ3 thay đổi trong khoảng từ -l đến l với chu kỳ trung bình khoảng 6 tháng.
Tương tự áp dụng cho Mặt Trăng, ta có a2.t + m.sin (2C) với C là kinh độ của Mặt Trăng.
Kết hợp hai kết quả trên, chuyển động của điểm phân được mô tả là: a + l.sin (2ʘ) + m.sin (2C) với a = a1 + a2
Điều giả tưởng ở trên xảy ra khi mặt phẳng quỹ đạo Mặt Trăng trùng với mặt phẳng hoàng đạo.Tuy nhiên quỹ đạo của nó lại nghiêng một góc i khoảng 5o,09 so với đường hoàng đạo. Bây giờ ta sẽ xét đến tác động của độ nghiêng đến chuyển động của điểm phân Ƴ.
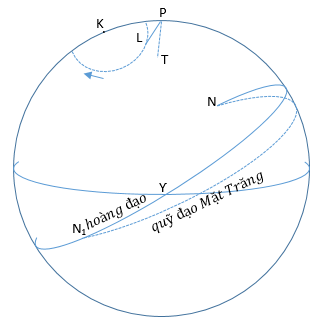Cho đường tròn cắt đường hoàng đạo tại N và N1 trên mặt phẳng quỹ đạo Mặt Trăng tại một thời điểm. Cực của mặt phẳng quỹ đạo Mặt Trăng là L. Khi đó KL là độ nghiêng i. Nếu L là cực trong khoảng thời gian rất ngắn là cố định trên thiên cầu. Tác động của lực hút của Mặt Trăng trên phỏng cầu Trái Đất là nguyên nhân là cực P chuyển động quanh L trong một vòng tròn nhỏ PT bán kính LP. Đầu tiên, nó dẫn đến một chuyển động giật lùi của Ƴ trên đường hoàng đạo. Thứ hai, khoảng cách góc giữa K và P không còn là một hằng số nữa và độ nghiêng giữa mặt phẳng hoàng đạo và mặt phẳng xích đạo là thay đổi. Từ lý thuyết động lực học, ta biết mặt phẳng quỹ đạo Mặt Trăng là không cố định so với đường hoàng đạo và chuyển động của cực L trên vòng tròn nhỏ quanh K với chu kỳ 18,6 năm. Ta thấy độ xa của Mặt Trăng có ảnh hưởng đến chuyển động của điểm phân Ƴ trên đường hoàng đạo. Nó được phân ra làm 2 thành phần: một là do chuyển động của Mặt Trăng giả sử như cực của quỹ đạo của nó trùng với K và mặt khác là do vị trí của mặt phẳng quỹ đạo Mặt Trăng đối với mặt phẳng hoàng đạo. Trên vị trí L, xác định vị trí kinh độ của nút N và N1 và độ nghiêng i. Thứ hai là chu kỳ của nó từ b.sin Ω + c.sin(2Ω) với Ω là kinh độ của điểm nút lên của Mặt Trăng và b, c là những hằng số trong thuyết động lực học.
Như vậy, chuyển động của điểm phân trên đường hoàng đạo được cho bởi:
a.t + b.sin Ω + c.sin(2Ω) + l.sin(2ʘ) + m.sin(2C)
Nó được gọi là chương động Mặt Trăng – Mặt Trời trong kinh độ. Tất cả những chu kỳ của của chương động như thế được gọi là chương động trong kinh độ Δψ.
Ta có, cực của mặt phẳng quỹ đạo Mặt Trăng không trùng với cực của mặt phẳng hoàng đạo, độ nghiêng của nó không phải là một hằng số. Chuyển động của L quanh K có tính chu kỳ, thay đổi trong độ nghiêng cũng có tính chu kỳ. Nếu Δε là thay đổi trong độ nghiêng, chu kỳ giới hạn của thay đổi là:
Δε = b1.cos Ω + c1.cos(2Ω) + l1.cos(2ʘ) + m1.cos(2C)
gọị là chương động trong độ nghiêng.
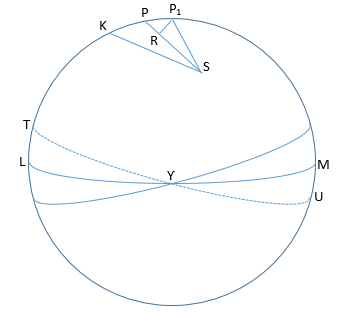Cho P là cực của đường xích đạo LƳM sau khi đã thêm tiến động Mặt Trăng- Mặt Trời. Cho P1 là cực của đường xích đạo TƳU khi thêm
chương động trong độ nghiêng. Cho tọa độ ngôi sao S tương ứng trên 2 đường xích đạo đó là (α,δ) và (α1,δ1). Do PS = 90o – δ, P1S = 90o – δ1, PK = ε, KP1 = ε + Δε, KPS = 90o + α, KP1S = 90o + α1, PKS = 90o – λ, KS = 90o – β. Từ P1 vẽ vòng tròn nhỏ sao cho cung P1R vuông góc PS. Do ε khá nhỏ nên ta có thể coi P1S = RS, PR = δ1– δ, P1PR = 90o – α.
PR = PP1.cos P1PR nên: δ1- δ = Δδ = Δε.sin α
Sử dụng công thức sine cho tam giác cầu KPS: cos α.cos δ = cos λ.cos β
Tương tự ta cũng có: cos α1.cos δ1 = cos λ.cos β
Từ α1 = α + Δα; δ1 = δ + Δδ, với độ chính xác vừa đủ ta có:
cos α1 = cos α – Δα.sin α và cos δ1 = cos δ – Δδ.sin δ
Khi đó: cos λ.cos β = cos α.cos δ – Δδ. cos α.sin δ – Δα.sin α.cos δ
Δα.sin α.cos δ = – Δδ. cos α.sin δ
Do đó: Δα = – Δε.cos α.tan δ
Tiến động hành tinh
Tại một điểm khi đường hoàng đạo cố đinh. Đầu tiên khảo sát một mặt phẳng cố định. Ngắm nhìn thiên vầu với tâm Mặt Trời. Bây giờ chúng ta cho 2 điểm nào đó trên thiên cầu (không đối lập nhau), có một và chỉ một vòng tròn lớn đi qua 2 điểm đó. Giả sử hai điểm đó là hai ngôi sao ở khoảng cách vô tận và đã tính đến thị sai, quang sai, chuyển động thực. Ta đặt mặt phẳng gồm Mặt Trời và 2 ngôi sao là cố định tương đối từ Mặt Trời. Do đó, mặt phẳng hoàng đạo là không cố định.
Cho đường hoàng đạo AƳB ở thời điểm 2000,0, nơi ta đã thừa nhận là mặt phẳng cố định. Đường hoàng đạo một năm sau đó là NCD, nơi nó giao với đường hoàng đạo cố định tại N. Thay đổi này của vị trí đường hoàng đạo là khá dài bởi lực hút của các hành tinh. Nó tăng lên theo biến thiên thế kỷ của độ nghiêng và trong kinh độ của điểm nút N của mặt phẳng quỹ đạo Trái Đất từ mặt phẳng cố định. Xét một cách riêng lẻ, điểm phân chuyển động trong một năm từ Ƴ tới C, chuyển động này của điểm phân gọi là tiến động hành tinh. Hiển nhiên, tác động của tiến động hành tinh dẫn đến một sự suy giảm trong
xích kinh của tất cả các ngôi sao trong khi không có sự thay đổi trong xích vĩ. Thực tế nó dựa trên sự biến đổi trong t năm của điểm phân Ƴ trên đường xích đạo với độ chính xác tương đối ct + dt2.