Hệ tọa độ Trái Đất

11/06/2019 | Mai Đức Thạch | 3378 xem

Hàng ngày, chúng ta đứng trên bề mặt Trái Đất để quan sát bầu trời, ta thấy dường như Mặt Trời, Mặt Trăng và các vì tinh tú như đang di chuyển trên bề mặt của một quả cầu với tâm là vị trí quan sát của chúng ta. Để mô tả vị trí của một thiên thể vào một thời điểm cụ thể, nhằm phục vụ cho mục đích quan sát, người ta đề ra một hệ thống các hệ tọa độ thiên văn.

Nhìn chung các hệ tọa độ thiên văn thông dụng đều là các hệ tọa độ cầu (tức là các tọa độ đều được đo bằng góc) và lấy thiên cầu làm hệ quy chiếu. Điểm mốc và mặt phẳng cơ sở đối với mỗi hệ tọa độ có cách chọn riêng. Do đó mà có nhiều hệ tọa độ thiên văn được sử dụng trong thiên văn học.

Khái niệm Tọa độ trên Trái Đất

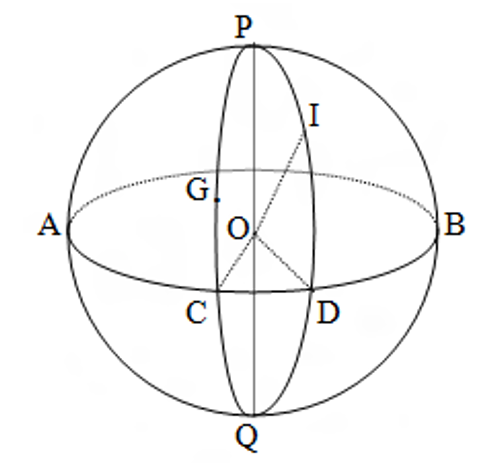
Hệ tọa độ Trái Đất

Giả sử Trái Đất là một quả cầu đường kính PQ với P là cực Bắc và Q là cực Nam. Vòng tròn lớn ACDB vuông góc với PQ là đường xích đạo. Nửa vòng tròn lớn đi qua P và Q gọi là một đường kinh tuyến. Đường kinh tuyến gốc PGCQ là đường kinh tuyến đi qua đài quan sát Greenwich (nước Anh) và cắt đường xích đạo tại C.

Đài thiên văn hoàng gia Greenwich được bắt đầu xây dựng vào ngày 10/8/1675 ở ngoại ô thủ đô Luân Đôn nước Anh với nhiệm vụ: “tính toán chi tiết sự chuyển động của các thiên thể, đo đạc vị trí của các ngôi sao trên thiên cầu và xác định chính xác các kinh tuyến nhằm phục vụ cho việc định hướng trong hàng hải”. Năm 1884, giờ Greenwich được công nhận là giờ chung của toàn thế giới. Hiện nay, nó là một bộ phận của bảo tàng quốc gia hàng hải Vương quốc Anh.

Cho I là một vị trí cụ thể trên bề mặt Trái Đất. Ta xác định một đường kinh tuyến đi qua I và cắt đường xích đạo tại D. Khi đó:

– Số đo của cung tròn CD trên đường xích đạo (hoặc là góc COD hay góc cầu GPI) ký hiệu là λ gọi là kinh độ của đường kinh tuyến PIQ. Nó nhận giá trị từ 0^o đến 180^o về phía Đông hoặc Tây đường kinh tuyến Greenwich. Tất cả những vị trí trên cùng một đường kinh tuyến thì có cùng kinh độ. Dựa trên kinh độ là cơ sở để xác định múi giờ trên Trái Đất.

– Số đo của cung tròn ID (hoặc góc IOD) ký hiệu ϕ gọi là vĩ độ của I. Nó nhận giá trị từ 0^o đến 90^o. Nếu I nằm giữa đường xích đạo và cực Bắc thì nó có vĩ độ Bắc, ngược lại nó sẽ nhận vĩ độ Nam. Số đo cung PI = 90^o – ϕ gọi là độ dư vĩ của I. Tất cả những vị trí có cùng vĩ độ thì cùng nằm trên một đường tròn nhỏ trên mặt phẳng song song với mặt phẳng xích đạo.

Vĩ độ địa tâm và vĩ độ thiên văn

Tuy nhiên hình dạng của Trái Đất không phải là hình cầu hoàn hảo mà thực chất nó có hình dạng phỏng cầu phình to ở đường xích đạo với bán trục nhỏ là đường thẳng nối hai cực của Trái Đất.

Vĩ độ địa lý và vĩ độ địa tâm

Cho một đường kinh tuyến của Trái Đất như POBQ, đó là một đường elip có trục lớn CB nằm trên mặt phẳng xích đạo (do đó, BC = a là bán kính xích đạo Trái Đất), bán trục nhỏ PC = b và độ lệch tâm của một đường kinh tuyến là e. Khi đó ta có: b² = a².(1 – e²). Phương trình đường elip POBQ trục Cx và Cy như hình vẽ có dạng:

$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$

Cho O là vị trí của quan sát, bỏ qua mọi sự lồi lõm của bề mặt Trái Đất, cho một đường thẳng vuông góc với tiếp tuyến bề mặt Trái Đất theo hướng DOZ, khi đó điểm Z được gọi là thiên đỉnh thiên văn của quan sát và một đường thẳng đi qua tâm Trái Đất (C) và O cắt thiên cầu tại Z’, khi đó điểm Z’ được gọi là thiên đỉnh địa tâm cho quan sát. Góc tạo bởi tia DZ tạo với bán trục chính góc Φ, khi đó góc Φ gọi là vĩ độ thiên văn; góc tạo bởi ta CZ’ và bán trục chính góc Φ’, khi đó góc Φ’ gọi là vĩ độ địa tâm; góc tạo bởi giữa thiên đỉnh thiên văn và thiên đỉnh địa tâm gọi là góc thiên đỉnh (ký hiệu v).

Cho x,y là tọa độ hình chữ nhật của O với các trục CB và CP. Ta có y/x = tan Φ’. Ta cũng có:

$\tan \phi =\frac{y}{x}.\frac{a^{2}}{b^{2}}$

Do đó:

$\frac{y}{x}=\tan \phi' =\frac{a^{2}}{b^{2}}.\tan \phi$

Thay trở lại phương trình đường elip ta có:

$\frac{x^{2}}{a^{2}}+x^{2}.\frac{b^{2}}{b^{4}}.tan^{2}\phi =1$

$\Rightarrow x^{2}=\frac{a^{4}.cos^{2}\phi }{a^{2}.cos^{2}\phi+b^{2}.sin^{2}\phi}$

mà b² = a².(1 – e²). Do đó:

$x^{2}=\frac{a^{2}.cos^{2}\phi }{1-e^{2}.sin^{2}\phi}$

Tương tự ta cũng có:

$y^{2}=\frac{a^{2}.(1-e^{2})^{2}.sin^{2}\phi }{1-e^{2}.sin^{2}\phi}$

Cho ρ = CO. Ta có: x = ρ.cos Φ’ và y = ρ.sin Φ’. Do đó:

$x=\rho .\cos \phi'=\frac{a.\cos \phi }{\sqrt{1-e^{2}.sin^{2}\phi}}$

$y=\rho .\sin \phi'=y^{2} =\frac{a.(1-e^{2}).\sin \phi }{\sqrt{1-e^{2}.sin^{2}\phi}}$

$\rho^{2}=\frac{a^{2}.(1-(2.e^{2}-e^{4}).\sin^{2} \phi) }{1-e^{2}.sin^{2}\phi}$

Nhân phương trình x với sin Φ và phương trình y với cos Φ và tính hiệu, với
v = Φ – Φ’:

$\rho.\sin v=\frac{a.e^{2}.\sin \phi.\cos \phi) }{\sqrt{1-e^{2}.sin^{2}\phi}}$

Nhân phương trình x với cos Φ và phương trình y với sin Φ và tính tổng:

$\rho.\cos v=a.\sqrt{1-e^{2}.\sin^{2} \phi}$

Từ hai phương trình ở trên ta có:

$\tan v=\frac{e^{2}.\sin(2.\phi)}{2.(1-e^{2}.\sin^{2} \phi)}=\frac{e^{2}.\sin(2.\phi)}{2-e^{2}+e^{2}.\cos (2.\phi))}$

Đặt $\frac{e^{2}}{2.-e^{2}}=m$ . Ta có $\tan v=\frac{m.\sin(2.\phi)}{1+m.\cos(2.\phi)}$

Bây giờ với e khoảng 0,08 và m khoảng 0,003, với độ chính xác cần thiết ta có:

$\frac{1+i.\tan v}{1-i.\tan v}=\frac{1+m.(\cos(2.\phi)+i.\sin(2.\phi))}{1+m.(\cos(2.\phi)-i.\sin(2.\phi))}$

Hoặc:

$e^{2.i.v}=\frac{1+m.e^{2.i.\phi}}{1+m.e^{-2.i.\phi}}$

$2.i.v=ln(1+m.e^{2.i.\phi})-ln(1+m.e^{-2.i.\phi})$

Khai triển logarit ta có:

$2.i.v=m.(e^{2.i.\phi}-e^{-2.i.\phi})-\frac{m^{2}}{2}.(e^{4.i.\phi}-e^{-4.i.\phi})+...$

$\Rightarrow v=m.\sin(2.\phi)-\frac{m^{2}}{2}.\sin(4.\phi)+...$

Với v tính theo giây cung, chúng ta có:

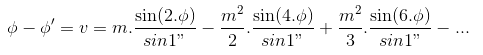
Tính khoảng cách vĩ độ địa lý và địa tâm

Ta có độ bẹt của mỗi đường kinh tuyến của Trái Đất là f được cho bởi:

$f=\frac{a-b}{a}=1-\sqrt{1-e^{2}}$

Theo quy ước của hiệp hội thiên văn quốc tế IAU năm 1964: a = 6378,160km và f = 1/298,25. Cho nên: b = 6356,7747 km ; e2 = 0,00669454 và m = 0,00335851. Vì vậy, ta có công thức:

$\phi-\phi'=v=692$

Nếu H là độ cao của quan sát trên mặt nước biển (tính bằng met), các đại lượng ρ.sin Ф’ và ρ.cos Ф’ cần được tính toán cho tính toán thị sai hàng năm, thiên thực và sự che khuất :

$\tan u=\frac{b}{a}.\tan \phi$