Nhật thực

25/06/2019 | Mai Đức Thạch | 592 xem

Khái niệm nhật thực

Nhật thực là một hiện tượng khi Mặt Trăng đi vào bên trong giữa Mặt Trời và Trái Đất. Khi Mặt Trăng ở trên hoặc gần vị trí giao hội với Mặt Trời, tức là vào thời kỳ trăng non. Cũng do độ nghiêng của quỹ đạo Mặt Trăng và đường hoàng đạo , nên một nhật thực không thể xuất hiện trừ khi Mặt Trăng phải ở trên hoặc gần đường hoàng đạo và phải ở gần hoặc ở trên điểm nút.

Do bán kính của Mặt Trăng nhỏ hơn rất nhiều so với bán kính Trái Đất, cho nên Trái Đất không thể nằm hoàn toàn trong vùng bóng của nó bởi vì Mặt Trời xa hơn Mặt Trăng rất nhiều, cho nên chỉ có thể quan sát được nhật thực trên một vùng xác định trên bề mặt Trái Đất.

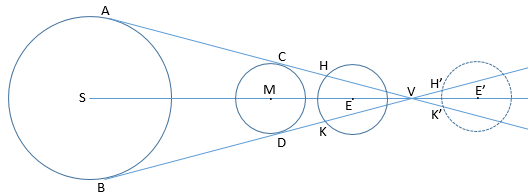
Khái niệm nhật thực

Trong hình vẽ trên, vùng bóng là vùng được giới hạn bởi hình nón phía trước đỉnh V, vùng nón này được gọi là vùng tối, còn vùng nón được xác định phía sau V được gọi là vùng nửa tối. Cho một điểm trên bề mặt Trái Đất ở khoảng giữa H và K, tức là vùng tối, Mặt Trăng sẽ che khuất hoàn toàn ánh sáng Mặt Trời và thiên thực này được gọi là nhật thực toàn phần. Nhưng đối với một điểm L trên bề mặt Trái Đất và nằm ngoài vùng tối, chỉ một phần đĩa
Mặt Trời bị che khuất, thiên thực đó được gọi là nhật thực một phần. Điều kiện để xảy ra nhật thực một phần là nó phải nằm trong vùng nửa tối.

Nhật thực toàn phần xảy ra tại tất cả các vị trí mà góc đường kính của Mặt Trăng lớn hơn góc đường kính của Mặt Trời (khi Mặt Trăng ở viễn điểm), trong trường hợp đĩa Mặt Trăng được bao bọc bởi đĩa Mặt Trời, khi đó thiên thực được gọi là nhật thực hình khuyên, như tại vị trí từ H’ và K’ như hình vẽ.

Góc đối diện tại tâm Trái Đất của Mặt Trăng và Mặt Trời khi bắt đầu hoặc kết thúc nhật thực

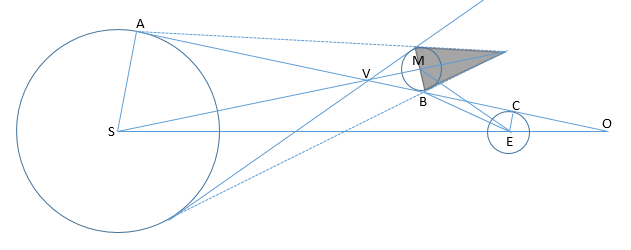
Cho tiếp tuyến AB tiếp xúc với bề mặt Trái Đất tại C. Khi đó tại vị trí quan sát C bề mặt Mặt Trời đang bắt đầu bị lấp, đánh dấu thời điểm bắt đầu hoặc kết thúc một giai đoạn nhật thực một phần. Đặt D là góc MES chúng ta có:

$D=\widehat{BES}+\widehat{MEB}$

Với MB gần như vuông góc với EB, khi đó $\widehat{MEB}=S_{1}$ , khi đó: $D=\widehat{BES}+S_{1}$

Nhưng $\widehat{BES}=\widehat{OBE}+\widehat{EOB}$ . Nhưng $\widehat{OBE}=\widehat{CBE}=$ thị sai chân trời của B, gần bằng thị sao xích đạo chân trời của M, do đó: $\widehat{OBE}=P_{1}$ . Trở lại:

$\widehat{EOB}=\widehat{EOA}=\widehat{AES}-\widehat{EAC}=S-P$

Do đó:

D = S + S₁ + P₁ – P

Giới hạn của nhật thực

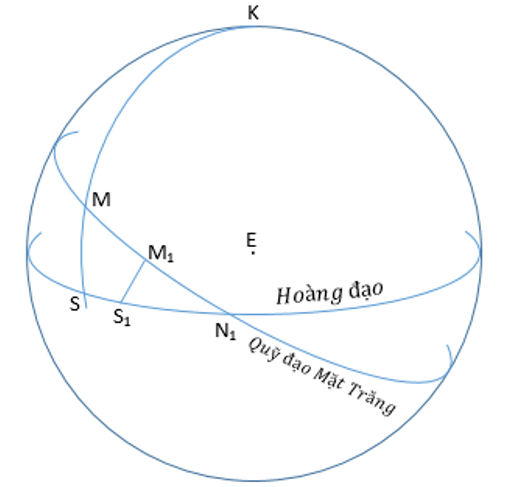
Trong hình vẽ trên cho Mặt Trời và Mặt Trăng có cùng kinh độ địa tâm tại M và S vào thời điểm trăng non – gần với điểm nút xuống N₁. Đặt β là vĩ độ SM và i là góc cầu MN₁S là độ nghiên của đường hoàng đạo và quỹ đạo Mặt Trăng. Đạt M₁ và S₁ là vị trí của Mặt Trăng và Mặt Trời tại thời điểm gần đó. Đặt MM₁ là y. Xét tam giác MN₁S như là một tam giác phẳng, chúng ta có kinh độ của Mặt Trăng MM₁.cos i hoặc y.cos i, và kinh độ của Mặt Trời SS₁. Nếu m là tỉ lệ SS₁ và y.cos i, chúng ta có:

SS₁ = m.y.cos i

Ta cũng có SN₁ = β.cot i và MN₁ = β.cosec i

Do đó:

S₁N₁ = β.cot i – m.y.cos i
M₁N₁ = β.cosec i – y

Đặt D là khoảng cách góc M₁S₁. Khi đó, ta xét tam giác M₁N₁S₁ như tam giác phẳng, chúng ta có:

D² = (β.cot i – m.y.cos i)² + (β.cosec i – y)² – 2.(β.cot i – m.y.cos i).(β.cosec i – y).cos i

$\Leftrightarrow D=(1-2.m.\cos^2 i+m^2.\cos^2 i).\left [ y-\frac{\beta.\sin{i}}{1-2.m.\cos^2 i+m^2.\cos^2 i} \right ]^2+\frac{\beta^2.(1-m)^2.\cos^2 i}{1-2.m.\cos^2 i+m^2.\cos^2 i}$

Giá trị nhỏ nhất của D là Do được cho bởi:

$\Leftrightarrow D=\frac{\beta.(1-m).\cos{i}}{(1-2.m.\cos^2 i+m^2.\cos^2 i)^{1/2}}=\frac{\beta.(1-m).\cos{i}}{(\sin^2 i+(1-m)^2.\cos^2 i)^{1/2}}$

Đặt góc j cho bởi:

$\tan{j}=\frac{\tan{i}}{1-m}$

Khi đó: $D_{o}=\beta.\cos{j}$ . Do tan i là một một đại lượng nhỏ (khoảng 1/11), từ i = 5^o,15 và m = 3/40. Chúng ta có:

cos j = cos I – 0,0006.cos i

Trong độ chính xác cần thiết:

$D_{o}=\beta.\cos{j}=\beta.\left ( 1-2.\sin^2 \frac{i}{2} \right )$

Để có một nhật thực, ta phải có điều kiện:

$\beta.\left ( 1-2.\sin^2 \frac{i}{2} \right )<S+S_{1}+P_{1}-P$

Do $\sin^2 \frac{i}{2}$ là một đại lượng nhỏ, nên ta có thể viết:

$\beta<S+S_{1}+P_{1}-P+2.(S+S_{1}+P_{1}-P).\sin^2 \frac{i}{2}$

Trong một giá trị tương đối: $\beta<S+S_{1}+P_{1}+0',2$

Giới hạn nhật thực ngoài được định nghĩa là khoảng cách lớn nhất của Mặt Trời đến điểm nút tại một thời điểm trăng non nếu một thiên thực xảy ra. Đặt x = SN₁. Chúng ta có:

sin x = tan β.cos i

x có giá trị lớn nhất khi β lớn nhất (1^o34’,8) và i nhỏ nhất (4^o58’,8). Khi đó x = 18^o,4. Khi đó, nếu khoảng cách của Mặt Trời từ nút tại thời điểm trăng non là 18^o,4, một nhật thực sẽ xuất hiện.

Để tính toán giới hạn nhật thực trong, chúng ta cần giá trị nhỏ nhất của β và giá trị lớn nhất của i. Giá trị nhỏ nhất của S, S₁ và P₁ tương ứng là 15’,8; 14’,7 và 53’,9. Khi đó, giá trị nhất của β là 1^o24’,6. Giá trị lớn nhất của i là 5^o18’,6. Khi đó, giới hạn nhật thực trong là 15^o,4. Do đó, nếu Mặt Trời cách nút 15^o,4 vào thời điểm trăng non, một nhật thực sẽ xuất hiện tại một nơi nào đó.

Các thông số Besselian cho một nhật thực

Thông số Besselian cho một nhật thực

Cho thiên cầu tâm Trái Đất E, cho đường thẳng EC như hình vẽ, tại thời điểm hiện tại, đường thẳng nối tâm Mặt Trăng và Mặt Trời cắt thiên cầu tại E từ C. EC là trục z và mặt phẳng DBA vuông góc với EC tại E là mặt phẳng cơ bản. Nếu P là thiên cực Bắc, mặt phẳng chứa vòng tròn lớn qua C và P giao với mặt phẳng cơ bản theo một giao tuyến EB. Ta lựa chọn EA và EB là trục x, y tương ứng.

– Thông số x, y và d:

Chúng ta gọi (α,δ) là xích kinh và xích vĩ biểu kiến của Mặt Trời và (α₁,δ₁) là tọa độ của Mặt Trăng.

Cho (a,d) là xích kinh và xích vĩ của điểm C trên thiên cầu.

Cho (x,y,z) là tọa độ hình chữ nhật của Mặt Trời trên các trục tọa độ, tính theo đơn vị bán kính Trái Đất. Khi đó, nếu X là vị trí của Mặt Trời trên thiên cầu, ta có:

x = r.cos AX
y = r.cos BX
z = r.cos CX

với R là khoảng cách địa tâm của Mặt Trời.

Bây giờ A là cực của vòng tròn lớn CPB và nằm trên đường xích đạo; chúng ta có: PA = 90^o, FA = 90^o. Khi đó xích kinh của A là 90^o + α và góc cầu XPA bằng 90^o + a – α; PX = 90^o – δ, sử dụng công thức cosine ta có:

x = r.cos δ.sin(α – a)

Trong tam giác PBX có BP = d, APX = 90^o, XPB = 180^o + a – α. Khi đó:

y = r.[sin δ.cos d – cos δ.sin d.cos(α – a)]

Trong tam giác PCX có PC = 90^o – d, PX = 90^o – δ và XPC = α – a. Khi đó:

z = r.[sin δ.sin d + cos δ.cos d.cos(α – a)]

Trong cách tính toán tương tự ta cũng có tọa độ xích đạo của Mặt Trăng:

x₁ = r₁.cos δ₁.sin(α₁ – a)
y₁ = r₁.[sin δ₁.cos d – cos δ₁.sin d.cos(α₁ – a)]
z₁ = r₁.[sin δ₁.sin d + cos δ₁.cos d.cos(α₁ – a)]

Nhưng từ việc trục z song song với đường thẳng nối tâm Mặt Trăng và Mặt Trời, chúng ta có: x = x₁ và y = y₁

Tọa độ (x,y) hoặc (x₁,y₁) là tọa độ tâm của vùng bóng trên mặt phẳng cơ bản. Khi đó:

r.cos δ.sin(α – a) = r1.cos δ1.sin(α1 – a)
r.[sin δ.cos d – cos δ.sin d.cos(α – a)] = r1.[sin δ1.cos d – cos δ1.sin d.cos(α1 – a)]

Tại một thời điểm nào đó, các giá trị r, r₁, α, δ, α₁, δ₁ đã được biết đến. Ta có thể tính được giá trị của a và d. Đặt một cách đơn giả tại thời điểm hoặc gần thời điểm xảy ra nhật thực (α,δ) khác với (α₁,δ₁) một lượng nhỏ, chúng ta có thể viết:

$\frac{r_{1}}{r}=b=\frac{\sin{P}}{\sin{P_{1}}}$

Do đó, b được xác định cho một thời điểm, nó có giá trị khoảng 1/400. Viết α1 – a = (α1 – α) + (α – a) ta có:

sin(α – a).[1-b.sec δ.cos δ₁.cos(α1 – α)] = b.sec δ.cos δ₁.cos(α1 – α).sin(α1 – α)

Từ đó, với độ chính xác cần thiết:

$a=\alpha -\frac{b.sec \delta .\cos{\delta_{1}}}{1-b}.(\alpha_{1}-\alpha)$

Với cách làm tương tự, chúng ta cũng có:

$d=\delta -\frac{b}{1-b}.(\delta_{1}-\delta)$

Từ đó ta tính được a và d đo trong đơn vị giờ.

Thêm vào đó, các đại lượng x’, y’ (mỗi giờ) là tọa độ (x,y) của tâm vùng búng dễ dàng tìm kiếm được thông qua x,y qua bảng trong lịch thiên văn.

– Thông số μ: góc giờ trên đường kinh tuyến của C là góc giờ của điểm xuân phân trừ đi xích kinh của C. Đặt μ là góc giờ của C cho kinh tuyến thiên văn khi giờ thiên văn là G, khi μ = G – a. Khi đó a là giá trị của μ tại một thời điểm nhất định. Giá trị của μ cũng được tính toán tương đối đơn giản.

– Thông số f₁ và f₂:

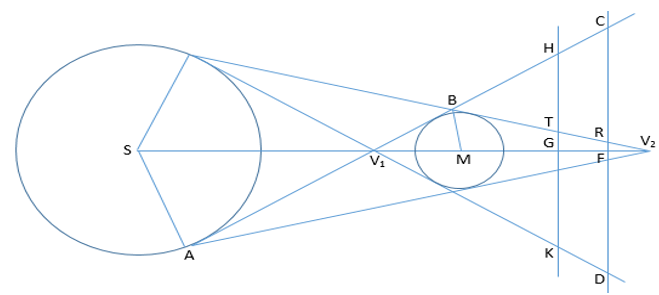
Thông số nhật thực

Trong hình vẽ trên, cho CD là mặt phẳng cơ bản nằm vuông góc với mặt giấy. Ta cho V₁ nằm giữa Mặt Trời và Mặt Trăng. Đặt f₁ là góc AV₁S hoặc FV₁C. Cho R là đường thẳng bán kính của Mặt Trời và k là của Mặt Trăng. Khi đó:

$\sin{f_{1}}=\frac{R}{SV_{1}}=\frac{k}{V_{1}M}=\frac{R+k}{SM}$

Nhưng trong suốt thời kỳ của thiên thực, SM = r – r₁, với độ chính xác cần thiết:

$\sin{f_{1}}=\frac{R+k}{r.(1-b)}$

Tương tự ta cũng có góc nón BV₂M gọi là f₂ cũng được xác định tương tự với công thức:

$\sin{f_{2}}=\frac{R-k}{r.(1-b)}$

– Thông số l₁ và l₂:

Trong hình vẽ trên, ta thấy MF là tọa độ z của tâm Mặt Trăng khi tham chiếu lên các trục tương ứng. Khi đó MF = z₁. Ta lại có V₁M = k.cosec f₁. Đặt V₁F là tọa độ trên trục z của nón của vùng nón nửa tối bởi c₁, chúng ta có:

c₁ = z₁ + k.cosec f₁

Tương tự, nếu c₂ là tọa độ của nón đỉnh V₂ của vùng tối, ta có:

c₂ = z2 – k.cosec f2

Đặt l₁ và l₂ là bán kính của đường tròn tạo bởi vùng nón nửa tối và vùng tối cắt mặt phẳng cơ bản. Khi đó:

l₁ = FC = c₁.tan f₁ = z₁.tan f₁ + k.sec f₁
l₂ = FR = c₂.tan f₂ = z₂.tan f₂ – k.sec f₂

Tính toán nhật thực cho một thời điểm cụ thể

Trong hình vẽ trên cho KH là nằm trên mặt phẳng vuông góc với mặt giấy và song song với mặt phẳng cơ bản. Cho (ξ,η,ζ) là tọa độ của quan sát tại một thời điểm khi chiếu lên các trục tọa độ. Khi đó, KH được cho bởi z = ζ. Bây giờ bán kính của đường tròn trên Mặt phẳng cơ bản là z = ζ cho bởi mặt phẳng này với nón nửa tối và tối. Đặt L₁ và L₂ là bán kính tương ứng của chúng. Trong hình vẽ L₁ = GH và L₂ = GT và FG = ζ. Ta có:

L₁ = (c₁ – ζ).tan f₁ = l₁ – ζ.tan f₁

L₂ = (c₂ – ζ).tan f₂ = l₂ – ζ.tan f₂

L₁ luôn luôn dương. L₂ là âm khi nón V₂ của vùng tối, điều này xảy ra khi điều kiện hình học vùng trên bề mặt Trái Đất có thể chìm trong vùng tối. Khi một quan sát cụ thể, khoảng cách ζ từ mặt phẳng cơ bản, nó là điều kiện cho một nhật thực toàn phần tại L₂ sẽ là âm.

Đặt ϕ’ và ρ là vĩ độ địa tâm và khoảng cách của người quan sát và λ là kinh độ phía Tây Greenwich của quan sát đó. Trong hình trước đó, cho X là thiên đỉnh địa tâm quan sát trên thiên cầu. Chúng ta có:

ξ = ρ.cos AX , η = ρ.cos BX , ζ = ρ.cos CX

Bây giờ, PX là kinh tuyến trên của quan sát và từ là góc giờ thiên văn của C, góc giờ của C cho quan sát là h là $\widehat{XPC}=\mu -\lambda -1,0027.\Delta T$ . Khi đó: $\widehat{XPA}=90^o-h$ , $PX=90^o-\phi'$ . Áp dụng công thức cosine cho tam giác cầu APX, ta có:

ξ = ρ.cos ϕ’.sin h

Chứng minh tương tự cho các công thức cho . Từ đây, ta có các công thức:

ξ = ρ.cos ϕ’.sin h
η = ρ.[sin ϕ’.cos d – cos ϕ’.sin d.cos h]
ζ = ρ.[sin ϕ’.sin d + cos ϕ’.cos d.cos h]

Cho ξ’, η’, ζ’ là sự thay đổi của ξ, η, ζ qua mỗi giờ. Chúng ta có:

ξ' = μ'.ρ.cos ϕ’.cos h
η' = μ'.ξ.sin d – ζ.d'

Bây giờ chúng ta sẽ tìm điều kiện bắt đầu và kết thúc một nhật thực một phần hoặc nhật thực toàn phần tại một địa điểm nào đó. Khi thời kỳ nhật thực một phần vừa mới bắt đầu hoặc kết thúc, quan sát sẽ thấy nó nằm trên đường viền của vùng nón nửa tối và khoảng cách của chúng từ trục của vùng bóng là L₁ – chính là bán kính của vòng tròn trên mặt phẳng z = ζ cắt vùng nón nửa tối. Nhưng tâm của vòng tròn có tọa độ là (x,y) và của tọa độ quan sát là
(ξ, η) và chúng có cùng tọa độ z do cùng nằm trên mặt phẳng song song với mặt phẳng cơ bản. Từ đây ta có phương trình:

$(x-\xi)^2+(y-\eta)^2=L_{1}^{2}$

Tương tự ta cũng có điều kiện để bắt đầu hoặc kết thúc thời kỳ toàn phần là:

$(x-\xi)^2+(y-\eta)^2=L_{2}^{2}$

Đầu tiên xét phương trình bắt đầu hoặc kết thúc thời kỳ nhật thực toàn phần. Chọn T là một thời điểm thích hợp theo giờ thiên văn gần thời điểm toàn phần, và cho T + t là giờ thiên văn thực sự lúc bắt đầu hoặc kết thúc thời kỳ toàn phần. Cho x_o,y_o là tọa độ hình chữ nhật của x,y tào thời điểm T và ξ_o, η_o là tọa độ quan sát vào thời điểm đó. Khi đó, chúng ta có, tại thời điểm T + t, tính bằng giờ chúng ta có:

x = x₀ + x'.t , y = y₀ + y'.t
ξ = ξ0 + ξ'.t , η = η0 + η'.t

Và L₂ = l₂ – ζ.tan f₂. Với việc f₂ là một góc nhỏ, nên giá trị của ζ.tan f₂ tại thời điểm T+t không khác lắm so với giá trị của nó vào thời điểm T; l₂ cũng là một đại lượng rất nhỏ. Với độ chính xác tương đối ta có thể lấy giá trị L₂ cho T. Như vậy, tại thời điểm bắt đầu hoặc kết thúc thời kỳ toàn phân hoặc hình khuyên:

$[x_{o}-\xi_{o}+t.(x'-\xi')]^2+[y_{o}-\eta_{o}+t.(y'-\eta')]^2=L_{1}^{2}$

Ở đây, tất cả các đại lượng đã biết, ta có thể tính được t cho thời điểm bắt đầu hoặc kết thúc thời kỳ toàn phần.

Đặt các đại lượng m, M, n, N như sau:

m.sin M = xo – ξo
m.cos M = yo – ηo
n.sin N = x' – ξ'
n.cos N = y' – η'

Ta thấy , do đó M có thể nhận 2 giá trị cách nhau 180^o, và giá trị của m là căn bậc hai của [(x_o – ξ_o)² + (y_o – η_o)²]. Chúng ta chọn giá trị của M sao cho sin M cùng dấu với (x_o – ξ_o). Một điều tương tự đối với n và N. Khi đó m và M là khoảng cách và vị trí góc của trục vùng bóng so với quan sát, n và N cũng vậy, nó thể hiện cho độ sáng và hướng của chuyển động của tâm bóng so với quan sát. Thay ngược trở lại, ta có phương trình:

$n^2.t^2+2.m.n.t.\cos{(M-N)}+m^2-L_{2}^{2}=0$

Phương trình này có 2 nghiệm thể hiện cho lúc bắt đầu và kết thúc của thời kỳ toàn phần. Đặt góc ψ sao cho:

L₂.sin ψ = m.sin(M – N)

Khi đó phương trình đã cho được biến đổi thành:

$n^2.t^2+2.m.n.t.\cos{(M-N)}+m^2.\cos^2(M-N)$
$=L_{2}^{2}-m^2+m^3.\cos^2(M-N)=L_{2}^{2}.\cos^2\psi$

Khi đó:

$t=-\frac{m}{n}.\cos{(M-N)}\pm \frac{L_{2}.\cos{\psi}}{n}$

Nếu $\tau =\frac{L_{2}.\cos{\psi}}{n}$ , thời điểm bắt đầu một nhật thực toàn phần theo giờ thiên văn là $T-\frac{m}{n}.\cos{\overline{M-N}}-\tau$ và thời điểm kết thúc một thiê thực toàn phần là $T-\frac{m}{n}.\cos{\overline{M-N}}+\tau$ .

Để có một giá trị chính xác hơn, ta có thể thay ngược lại giá trị t này đến khi đạt được độ chính xác cao nhất mà bạn mong muốn. Tiến hành tương tự đối với phương trình thứ nhất để có thời gian bắt đầu và kết thúc thiên thực một phần.

Facebook