Nguyệt thực

25/06/2019 | Mai Đức Thạch | 555 xem

Khái niệm nguyệt thực

Một nguyệt thực xảy ra khi Mặt Trăng đi qua vùng bóng (trong mối quan hệ với ánh sáng từ Mặt Trời) nhìn từ Trái Đất. Điều này chỉ xảy ra khi Trái Đất nằm ở giữa Mặt Trời và Mặt Trăng, tức là khi Mặt Trăng ở vị trí đối lập, tức là vào khoảng thời kỳ ‘Trăng tròn’.

Nếu quỹ đạo Mặt Trăng đồng nhất với đường hoàng đạo, nguyệt thực sẽ xảy ra vào tất cả những khi ‘trăng tròn’; nhưng do mặt phẳng này nghiêng một góc khoảng 5o so với đường hoàng đạo, cho nên điều kiện để xảy ra một nguyệt thực là khi Măt Trăng ở trên hoặc gần đường hoàng đạo vào thời kỳ Trăng tròn, tức là khi Mặt Trăng phải ở trên hoặc gần điểm nút.

Khi đĩa Mặt Trăng hoàn toàn đi vào vùng bóng, nguyệt thực được gọi là nguyệt thực toàn phần, khi chỉ một phần của nó đi vào vùng bóng, ta gọi đó là nguyệt thực một phần.

Khái niệm Nguyệt thực

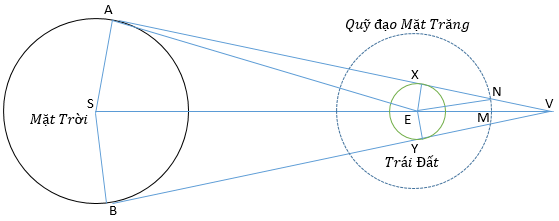
Trong hình vẽ trên S và E là tâm của Mặt Trời và Trái Đất. Một vùng nón được tạo ra bởi tiếp tuyến của bề mặt của Mặt Trời và Trái Đất với đỉnh V, và phần nón giữa XV và YV gọi là vùng vùng tối. Trong hình vẽ, thể hiện quỹ đạo của Mặt Trăng, nếu Mặt Trăng đi vào vùng tối thì một nguyệt thực toàn phần sẽ xảy ra.

Tiếp theo, ta xét vùng nón được tạo bởi các tiếp tuyến của bề mặt của Mặt Trời và Trái Đất với đỉnh W, phần nón được giới hạn bởi DXV và CYV được gọi là vùng nửa tối và khi Mặt Trăng đi qua vùng nòn này thì một nguyệt thực một phần sẽ xảy ra.

Góc bán kính của vùng bóng tại khoảng cách địa tâm của Mặt Trăng

Trong phần này chúng ta cần sử dụng những đại lượng sau:

– P, P₁ : thị sai xích đạo chân trời của Mặt Trời và Mặt Trăng.

– S, S₁ : bán kính đĩa Mặt Trời và Mặt Trăng.

– r, r₁ : khoảng cách địa tâm của Mặt Trời và Mặt Trăng tính theo đơn vị bán kính xích đạo Trái Đất.

– s : góc bán kính (nhìn từ tâm Trái Đất) của vùng nón tối tại khoảng cách Mặt Trăng.

Góc bán kính của vùng bóng tại khoảng cách địa tâm của Mặt Trăng

Bán kính của vùng nón tối tại khoảng cách của Mặt Trăng khi một nguyệt thực toàn phần xảy ra là MN, góc bán kính s, nhìn từ E là $\widehat{NEM}$ . Đặt $v=\widehat{XVE}$ . Khi đó, ta có: $\widehat{XNE}=s+v$ . Nhưng $\widehat{XNE}$ là góc nhìn từ bên ngoài của Mặt Trăng nhìn bán kính Trái Đất, giả định như Trái Đất là hình cầu, chúng ta có: $\widehat{XNE}=P_{1}$ . Khi đó:

P₁ = s + v

Trở lại, $\widehat{SEA}=\widehat{XAE}+v$ . Nhưng SEA là góc bên ngoài của Trái Đất chắn bởi bán kính Mặt Trời do đó nó là góc bán kính S. Ta lại có là thị sai của Mặt Trời P. Khi đó:

S = P + v

Như vậy, ta có:

s = P + P₁ – S

Tương tự cách làm như trên, ta cũng dễ dàng có được góc bán kính s’ của nón vùng nửa tối được cho bởi:

s' = P + P1 + S

Bây giờ tính đến ảnh hưởng của khúc xạ ánh sáng đến hai công thức trên, theo lý thuyết là khoảng 2%. Hai công thức cho nguyệt thực ở trên được đưa về dạng:

$s=\frac{51}{50}.(P+P_{1}-S)$

$s'=\frac{51}{50}.(P+P_{1}+S)$

Ví dụ: chúng ta có các giá trị P = 9”, P1 = 57’, S = 16’. Ta sẽ tính được s = 42’. Khí đó góc đường kính của vùng tối là 84’. Nếu trong thời kỳ nguyệt thực toàn phần, do đó nếu trục EV của vùng nón bóng đi qua tâm Mặt Trăng. Khi đó tâm Mặt Trăng chuyển động qua góc 84’ – 2S₁ hoặc 52’ nếu S₁ = 16’. Bây giờ nếu khoảng cách giữa hai lần trăng tròn là khoảng 30 ngày, khi đó góc chuyển động tương đối của Mặt Trăng là khoảng 12^o mỗi ngày (hoặc 30’). Khi đó trung tâm nguyệt thực sẽ khoảng 52/30 giờ.

Giá trị của s lớn nhất 46’,7 tới nhỏ nhất 38’,5. Giá trị lớn nhất xảy ra khi Mặt Trăng gần Trái Đất nhất tại cùng thời điểm Trái Đất xa Mặt Trời nhất và giá trị nhỏ nhất xảy ra khi Mặt Trăng ở viễn điểm và Trái Đất ở cận điểm.

Chiều dài của EV dễ dàng được tính toán: EV = EX.cosec(S – P).

Trong ví dụ trên ta sẽ tính được EV = 859000m với EX = 3960m.

Giới hạn của nguyệt thực

Bây giờ chúng ta xét đến tác động của độ nghiêng của đường Hoàng đạo và mặt phẳng quỹ đạo của Mặt Trăng đến nguyệt thực.

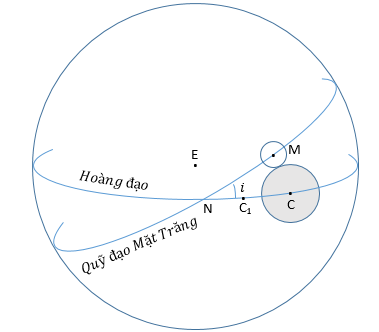
Giới hạn của nguyệt thực

Trong hình vẽ trên, cho một thiên cầu địa tâm E, NM là vòng tròn lớn nằm trên mặt phẳng quỹ đạo của Mặt Trăng. Cho M và C là tâm của Mặt Trăng và bóng của nó khi một nguyệt thực sắp xảy ra. Cho C1 là tâm của bóng của Mặt Trăng khi Mặt Trăng tại điểm nút N. Đặt NC₁ bởi ξ và t là thời gian Mặt Trăng di chuyển từ N tới M và cho tâm của bóng đi từ C₁ đến C. Bây giờ, kinh độ địa tâm của C bằng kinh độ của Mặt Trời cộng 180^o. Khi đó, chúng ta cần tìm giá trị lớn nhất của ξ nơi mà nguyệt thực còn tồn tại, bên cạnh đó tìm giá trị khoảng cách góc lớn nhất của Mặt Trời từ nút khác.

Cho là tốc độ thay đổi của kinh độ của Mặt Trời và là vận tốc góc của Mặt Trăng trên quỹ đạo của nó, để đơn giản chúng ta coi là những hằng số. Khi đó:

$NM=\dot{\phi}.t, NC=\xi +\dot{\theta }.t$

Cho η là khoảng cách góc CM và I là góc MNC, chúng ta có, xét tam giác MNC như tam giác phẳng,

$\eta^2=(\xi+\dot{\theta}.t)^2+\dot{\phi}^2.t^2-2.\dot{\phi}.t.(\xi+\dot{\theta}.t).\cos{i}$

$\eta^2=\xi^2-2.\xi.t.(\dot{\phi}.\cos{i}-\dot{\theta})+t^2.(\dot{\theta}^2+\dot{\phi}^2-2.\dot{\phi}.\dot{\theta}.\cos{i})$

Khi η là một đại lượng nhỏ. Khi đó t được cho bởi:

$\xi.(\dot{\phi}.\cos{i}-\dot{\theta})-t.(\dot{\theta}^2+\dot{\phi}^2-2.\dot{\phi}.\dot{\theta}.\cos{i})=0$

Gọi giá trị nhỏ nhất η_o, chúng ta có:

$\eta_{o}=\frac{\xi.\dot{\phi}.\sin{i}}{(\dot{\theta}^2+\dot{\phi}^2-2.\dot{\phi}.\dot{\theta}.\cos{i})^{1/2}}$

Đặt $q=\dot{\theta}/\dot{\phi}$ chúng ta có thể viết:

$\xi=\eta_{o}.(1-2.q.\cos{i}+q^2)^{1/2}.cosec i$

Bây giờ q là tỉ lệ tốc độ góc của quỹ đạo Trái Đất và vận tốc góc của quỹ đạo Mặt Trăng hoặc cũng chính là tye lệ chu kỳ thiên văn của Mặt Trăng tính theo năm. Với một giá trị chính xác vừa đủ lấy q khoảng 3/40 và i = 5^o,15. Khi đó: $\xi=10,3.\eta_{o}$ . Nếu Mặt Trăng ở khoảng tâm của vùng nón tối, .

Cho một nguyệt thực một phần không vượt quá 10,3.(s+S₁) và cho một nguyệt thực toàn phần không vượt quá 10,3.(s-S₁).

Ví dụ, chúng ta có S = 960”, S₁ = 933”, P = 9”, P₁ = 3423”. Đối với một nguyệt thức một phần ξ < 9^o,9 và đối với một nguyệt thực toàn phần ξ < 4^o,6.

Giá trị của nguyệt thực trong vùng nửa bóng được tính toán tương tự.

Giải pháp trong ví dụ này dung để xem xét điều kiện để xảy ra một nguyệt thực. Nó xác định vị trí lớn nhất trong mối tương quan với Mặt Trời từ điểm nút tại thời điểm kinh độ đối lập (trăng tròn). Từ tất cả những điều nói trên ta thấy giá trị lớn nhất là 12^o,3 (giới hạn thiên thực ngoài) và giá trị nhỏ nhất 9^o,6 (gọi là giới hạn thiên thực trong).

Tính toán một nguyệt thực

Chúng ta sẽ tìm điều kiện cho một nguyệt thực một phần hoặc toàn phần xuất hiện.

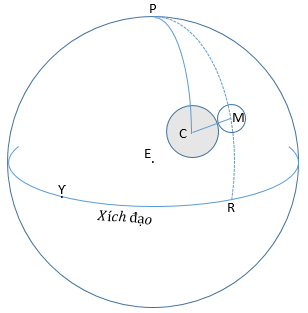
Tính toán một nguyệt thực

Cho M là vị trí của Mặt Trăng trên thiên cầu tâm E, và C là bóng tâm của Trái Đất. Cho (α₁;δ₁) và (α_o;δ_o) là tọa độ xích đạo của tâm Mặt Trăng và C. Đặt η là số đo cung CM và Q là góc cầu PCM. Chúng ta có:

sin η.sin Q = cos δ₁.sin(α₁ – α_o)
sin η.cos Q = sin δ₁.cos δ_o– cos δ₁.sin δ_o.cos(α₁ – α_o)

Với một độ chính xác tương đối, ta có:

η.sin Q = (α₁ – α_o).cos δ₁
η.cos Q = δ₁ – δ_o

Với C là vị trí đối lập của tâm Mặt Trời cho nên RA α_o của C bằng RA của Mặt Trời +12^h, và xích kinh δ_o của C bằng -δ (với δ là kinh độ của Mặt Trời). Khi đó chúng ta có thể viết:

x = η.sin Q = (α₁ – α_o).cos δ₁
y = η.cos Q = δ₁ – δ_o

Đặt x’ và y’ là tốc độ thay đổi của x và y, với x và y được tính theo đơn vị giờ trong thời điểm xảy ra thiên thực. Cho T_o là thời điểm gần với vị trí hiện tạo. Cho x_o và y_o là giá trị của x vày tại thời điểm hiện tại. tại ET (T_o + t) chúng ta có thể viết:

x = x’.t, y = y_o + y’.t

Đặt x_o = m.sin M; y_o = m.cos M và x’ = n.sin N; y’ = n.cos N. Ta có:

η.sin Q = m.sin M + n.t.sin N
η.cos Q = m.cos M + n.t.cos N

Bình phương cả hai phương trình trên rồi cộng với nhau, ta được:

η² = m² + 2.m.n.t.cos(M-N) + n².t²

Từ đó, ta tính được t:

$t=-\frac{m}{n}.\cos{(M-N)}\pm \left [ \frac{\eta^2-m^2.\sin^2{(M-N)}}{n^2} \right ]^{1/2}$

Đặt m.sin(M – N) = η.sin ψ. Ta có:

$t=-\frac{m}{n}.\cos{(M-N)}\pm \frac{\eta}{n}.\cos{\psi}$

Thay giá trị η trong điều kiện xảy ra một nguyệt thực khi Mặt Trăng bắt đầu đi vào vùng bóng là 51/50.(P + P₁ – S) + S₁; khi bắt đầu và kết thúc nguyệt thực toàn phần là 51/50.(P + P₁ – S) – S₁.

Thời điểm trung tâm của nguyệt thực một phần và toàn phần được cho bởi T_o + t’ với:

$t'=-\frac{m}{n}.\cos{(M-N)}$

Độ sáng của một thiên thực một phần của đĩa Mặt Trăng được cho bởi:

$\frac{\eta-m.\sin{(M-N)}}{2.S_{1}}$

Bây giờ chúng ta xem xét vị trí góc của điểm trên đĩa Mặt Trăng khi bắt đầu hoặc kết thúc nguyệt thực, trong hình vẽ trên, ta thấy khi Mặt Trăng đi vào vùng bóng, vẽ một vòng tròn lớn nối điểm tâm địa Mặt Trăng với tâm của bóng Trái Đất và tâm của vùng bóng có một góc PMC với kinh tuyến PM qua đĩa Mặt Trăng.Ta có vị trí góc θ cho bởi:

$\theta=360^{o}-\widehat{PMC}=180^{o}+\widehat{CMR}$