Đường Conic
 Điểm và vectơ
Điểm và vectơ
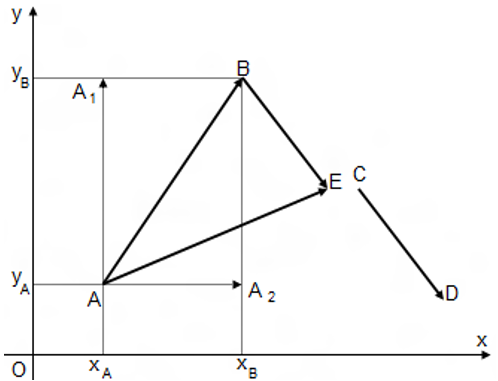
Trong hệ tọa độ Đê các hai chiều, một điểm A có tọa độ xA, yA được ký hiệu A(xA;yA), tức là từ điểm A chiếu xuống trục Ox nó có hoành độ xA, chiếu xuống trục Oy nó có tung độ yA.
Tọa độ của vectơ AB là xAB;yAB được ký hiệu là là tọa độ của điểm B khi đã chuyển gốc tọa độ đến A và các trục AA1, AA2 có phương và hướng như hệ tọa độ Oxy.
Ta có A(xA;yA) và B(xB;yB). Khi đó:
và
Cho và
:
• Tổng của hai vectơ:
Ta có:
• Tích vô hướng của hai vectơ:
Đường thẳng
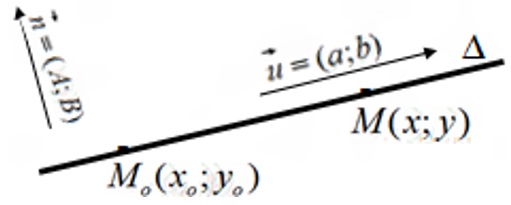 Phương trình đường thẳng:
Phương trình đường thẳng:
Yêu cầu: Viết phương trình đường thẳng ∆ khi biết M(x0;y0) nằm trên ∆ và vectơ pháp tuyến và vectơ chỉ phương
.
Cho M(x;y) là một điểm di động trên ∆.
• Phương trình tổng quát:
Ta có: và
. Ta có
nên ta có
. Khi đó ta có:
Ta có và
cùng phương nên ta có
với t thuộc R.
• Phương trình chính tắc:
Từ phương trình tham số của ∆ ta có:
• Phương trình tọa độ cực:
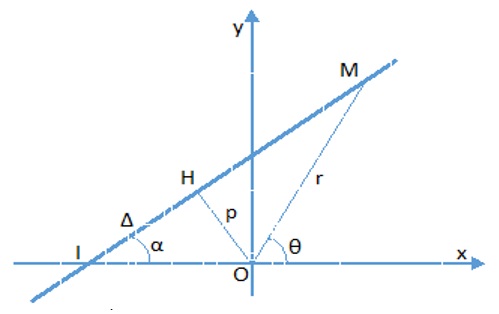 Ta có α là góc giữa đường thẳng Δ và trục Ox; r là khoảng cách góc từ một điểm M bất kỳ trên đường thẳng đến gốc tọa độ; θ là góc giữa MO và trục Ox; p là khoảng cách từ gốc tọa độ đến đường thẳng.
Ta có α là góc giữa đường thẳng Δ và trục Ox; r là khoảng cách góc từ một điểm M bất kỳ trên đường thẳng đến gốc tọa độ; θ là góc giữa MO và trục Ox; p là khoảng cách từ gốc tọa độ đến đường thẳng.
Khi M di chuyển trên Δ thì góc θ và độ dài r thay đổi. Ta cần tìm mối quan hệ giữa chúng.
Trong ΔOMH vuông tại H có OH = p; OM = r;
Ta có: nên:
r = p.csc(θ – α)
Ngoài ra chúng ta thường gặp một số dạng khác của phương trình đường thẳng:

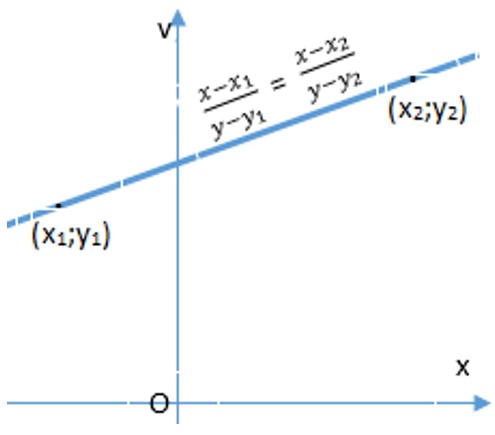
Một số bài toán liên quan đến đường thẳng
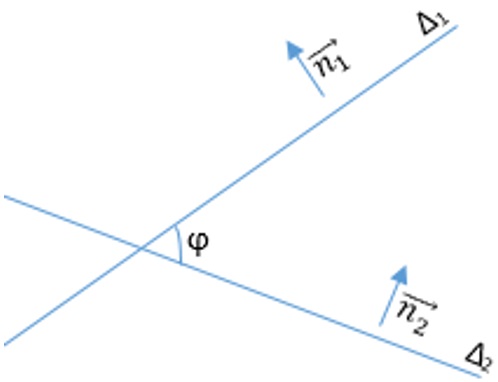 ● Góc giữa hai đường thẳng (Δ1): A1.x + B1.y + C1 = 0 và (Δ2): A2.x + B2.y + C2 = 0
● Góc giữa hai đường thẳng (Δ1): A1.x + B1.y + C1 = 0 và (Δ2): A2.x + B2.y + C2 = 0
Ta có vectơ pháp tuyến của 2 đường thẳng trên lần lượt là: và
![]() .
.
Góc giữa hai đường thẳng Δ1 và Δ2 là góc giữa hai vectơ pháp tuyến
và
![]() .
.
Khi đó:
Do đó:
 ● Khoảng cách tử một điểm đến một đường thẳng:
● Khoảng cách tử một điểm đến một đường thẳng:
Cho đường thẳng Δ: A.x + B.y + C = 0 và điểm M(xo;yo). H là hình chiếu của M xuống Δ. Ta có: d(M, Δ) = MH.
Đường thẳng Δ có nó là vectơ chỉ phương của đường thẳng MH. Do đó, ta có phương trình đường thẳng MH là:
Gọi (x1;y1) là tọa độ của H, ta có:
Ta lại có:
Như vậy:
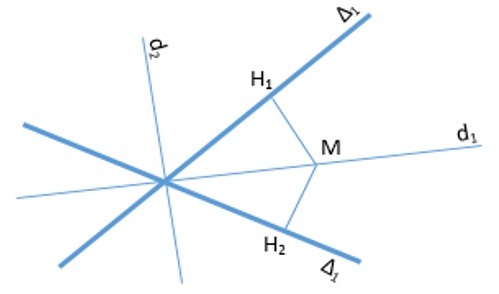 ● Phương trình đường phân giác của hai đường thẳng (Δ1): A1.x + B1.y + C1 = 0 và (Δ2): A2.x + B2.y + C2 = 0.
● Phương trình đường phân giác của hai đường thẳng (Δ1): A1.x + B1.y + C1 = 0 và (Δ2): A2.x + B2.y + C2 = 0.
Ta cho điểm M(x,y) là một điểm nằm trên đường phân giác của hai đường thẳng trên.
Ta có: d(M, Δ1) = d(M, Δ2)
Đưa bài toán về dạng tìm quỹ tích điểm M, ta có:
Đó là phương trình đường phân giác trong và ngoài hai đường thẳng đã cho.
Đường tròn
Phương trình đường tròn
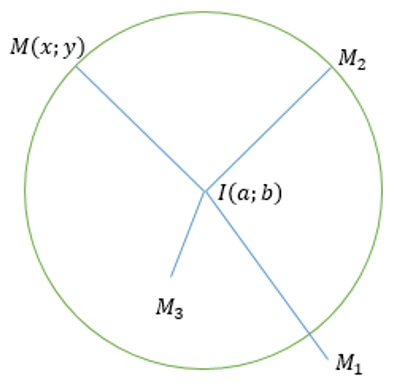 Cho đường tròn (C) tâm I(a;b) bán kính R và một điểm M(x;y) di động trên đường tròn. Ta có IM = R.
Cho đường tròn (C) tâm I(a;b) bán kính R và một điểm M(x;y) di động trên đường tròn. Ta có IM = R.
Ở dạng tổng quát, ta có:
x2 + y2 + 2.A.x + 2.B.y + C = 0 với A2 + B2 – C >0
là phương trình đường tròn tâm I(-A;-B) bán kính .
Phương tích của một điểm đối với một đường tròn
Cho đường tròn (C): x2 + y2 + 2.a.x + 2.b.y + c = 0 và điểm M(xo; yo). Ta có:
PM/(C) = MO2 – R2 với O(-a; -b) và nên:
Từ đây, ta có:
+ Nếu f(xo;yo) > 0 : điểm M nằm ngoài đường tròn.
+ Nếu f(xo;yo) = 0 : điểm M nằm trên đường tròn.
+ Nếu f(xo;yo) < 0 : điểm M nằm trong đường tròn.
Trục đẳng phương của hai đường tròn
Cho hai đường tròn không đồng tâm: (C1): x2 + y2 + 2.a1.x + 2.b1.y + c1 = 0 và (C2): x2 + y2 + 2.a2.x + 2.b2.y + c2 = 0
Điểm M(x;y) nằm trên trục đẳng phương của hai đường tròn (C1) và (C2), ta có:
PM/(C1) = PM/(C2) => x2 + y2 + 2.a1.x + 2.b1.y + c1 = x2 + y2 + 2.a2.x + 2.b2.y + c2
Ta có: 2(a1 – a2)x + 2(b1 – b2)y + c1 – c2 = 0
Elip
Định nghĩa: Elip là quỹ tích các điểm mà tổng khoảng cách của chúng đến 2 điểm cố định là không đổi.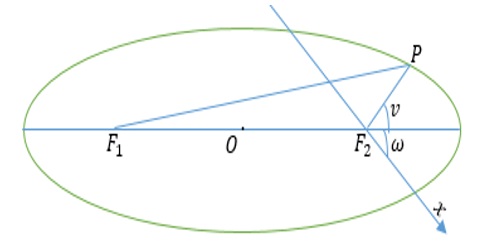
Trong hình vẽ bên:
A1A2 là trục lớn (=2.a)
B1B2 là trục nhỏ (=2.b)
F1F2 là tiêu cự (=2.a.e) với F1, F2 là 2 tiêu điểm.
Tâm sai:
Độ dẹt:
Bán trục qua tiêu F1H = l = a.(1 – e2)
Phương trình đường elip
● Phương trình chính tắc
Ta có F1(-ae;0) và F2(ae;0). Cho P(x;y) là một điểm di động trên elip.Sử dụng định nghĩa elip ta có: PF1 + PF2 = 2a
. Rút gọn biểu thức ta được:
với
và
● Phương trình tham số
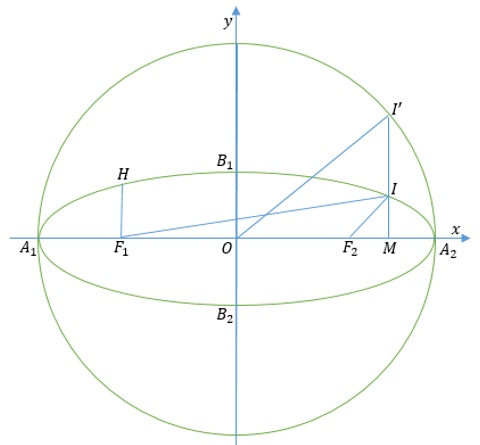 Ta vẽ đường tròn tâm O, bán kính a. M là hình chiếu của điểm I(x;y) xuống trục Ox. Tia MI cắt đường tròn (O;a) tại I’. Khi đó: x = OM; a = OI’; Đặt góc I’OA2 là E gọi là khoảng cách góc lệch tâm. Ta có:
Ta vẽ đường tròn tâm O, bán kính a. M là hình chiếu của điểm I(x;y) xuống trục Ox. Tia MI cắt đường tròn (O;a) tại I’. Khi đó: x = OM; a = OI’; Đặt góc I’OA2 là E gọi là khoảng cách góc lệch tâm. Ta có: nên x = a.cos E. Thay trở lại phương trình chính tắc ta được y = b.sin E. Từ đó, ta có phương trình tham số của elip:
Trong tam giác vuông IF2M có IF2 = r; IM = y = b.sin E; F2M = OM – OF2 = a.cos E – a.e = a.(cos E – e). Ta có:
![]()
Như vậy:
r = a.(1 – e.cos E)
Ta lại có![]()
là khoảng cách góc thật. Ta có:
Biến đổi lượng giác thông thường ta cũng có:
và
và
● Phương trình tọa độ cực
Trong phương trình tọa độ cực này, ta chọn chục x nghiêng với trục lớn góc ω. Một điểm P trên elip có vectơ bán kính F2P = r; nghiêng với trục lớn góc v. Ta đặt θ = ω + v gọi là góc tọa độ cực. Áp dụng công thức cosin cho tam giác phẳng PF1F2, ta có:
Như vậy:
Tiếp tuyến của elip
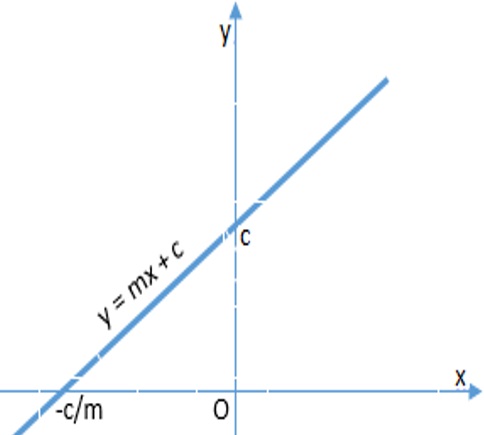
● Tìm c để đường thẳng y = mx + c tiếp xúc với elip
Ta có hoành độ giao điểm của elip và đường thẳng trên là nghiệm của phương trình:
(a2.m2 + b2).x2 + 2.a2.c.m.x + a2.(c2 – b2) = 0
Để tiếp xúc với elip phương trình trên phải có nghiệm duy nhất khi c2 = a2.m2 + b2. Khi đó phương trình tiếp tuyến của elip có dạng: tương đương với:
m2.(a2 – x2) + 2.m.y + b2 – y2 = 0
Bây giờ tìm đường thẳng vuông góc với đường thẳng trên đồng thời cũng tiếp xúc với elip. Làm tương tự ta cũng có:
m2.(b2 – y2) + 2.m.x + a2 – x2 = 0
Cộng hai phương trình tiếp tuyến trên với nhau ta được:
Dấu ‘=’ xảy ra khi và chỉ khi x2 + y2 = a2 + b2. Như vậy quỹ tích các điểm mà từ đó kẻ được hai tiếp tuyến vuông góc vớinh au là một đường tròn bán kính .
● Phương trình tiếp tuyến tại một điểm. Ta gọi K(xo;yo) là một điểm trên elip mà tiếp tuyến y = mx + c đi qua. Ta có:
Đường chuẩn của elip
 Ta có hai đường thẳng
Ta có hai đường thẳng là những đường chuẩn của elip.Ta có:
PN = P1N1 = ON1 – OP1 = a/e – a.cos E
PF2 = a.(1 – e.cos E)
Nên : PF2/PN = e
- Đường kính liên hợp là một đường elip có trục nhỏ và trục lớn không vuông góc với nhau.
Hyperbol
 Định nghĩa: Hyperbol là quỹ tích các điểm mà hiệu khoảng cách từ nó đến hai điểm cố định là không thay đổi.
Định nghĩa: Hyperbol là quỹ tích các điểm mà hiệu khoảng cách từ nó đến hai điểm cố định là không thay đổi.
Ta có:
A1A2 : là trục thực (=2.a);
B1B2 : là trục ảo;
F1F2 : là tiêu cự (=2.a.e) với F1và F2 là hai tiêu điểm;
Tâm sai: ;
F1H = l = a.(e2 – 1) là bán kính qua tiêu;
Hai đường tiệm cận: .
Phương trình Hyperbol
● Phương trình chính tắc: Ta có F1(-ae;0) và F2(ae;0). Điểm P(x;y) di động trên Hyperbol. Sử dụng định nghĩa ta có:
với
Ta cũng có phương trình liên hợp của Hyperbol là:
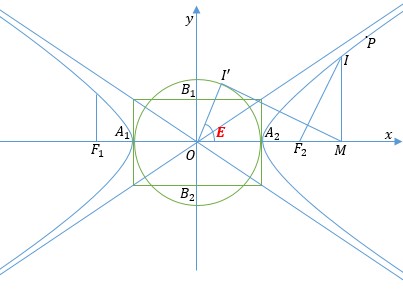
● Phương trình tham số: Cho đường tròn tâm O bán kính a. Cho I(x;y) là một điểm tùy ý trên Hyperbol và M là hình chiếu của nó xuống trục Ox. Kẻ tiếp tuyến MI’ với đường tròn (O;a). Đặt góc I’OA2 là E. Ta có OI’ = a; OM = x. Ta có cos E = OI’/OM = a/x nên:
x = a.sec E. Thay x vào phương trình chính tắc ta được: y = b.tan E. Ta có phương trình:
● Phương trình tọa độ cực: ta cũng lấy trục x nghiêng với trục thức góc ω với gốc tại tiêu điểm F2; v là khoảng cách góc thật. Ta có θ = ω + v là góc tọa độ cực. Sử dụng công thức cosin cho tam giác phẳng F1IF2,ta có:
Như vậy:
Tiếp tuyến của Hyperbol
Tiến hành tương tự như đối với elip, ta thấy đường thẳng y = mx+ c là tiếp tuyến của Hyperbol khi và chỉ khi .
Và tiếp tuyến của Hyperbol tại điểm (x1; y1) trên Hyperbol có phương trình là . Vòng tròn lớn, nơi mà từ một điểm trên nó có thể kẻ được hai tiếp tuyến vuông góc với nhau có bán kính
.
Các đường chuẩn của Hyperbol có phương trình
Parabol
 Định nghĩa: Parabol là quỹ tích các điểm mà khoảng cách từ nó đến một đường thẳng cố định và một điểm cố định là không đổi.
Định nghĩa: Parabol là quỹ tích các điểm mà khoảng cách từ nó đến một đường thẳng cố định và một điểm cố định là không đổi.
F(q;0) là tiêu điểm;
Đường chuẩn (Δ): x = -q;
Bán trục qua tiêu: FH = l = 2q;
Trục chính OF = q;
Phương trình Parabol:
● Phương trình chính tắc: Từ định nghĩa Parabol ta có: PF = PN nên:
(x – q)2 + y 2 = (x + q)2 tương đương với y2 = 4qx
● Phương trình tham số của Parabol:
● Phương trình tọa độ cực:
Ta lấy trục x nghiêng với trục chính góc ω, vectơ bán kính PF nghiêng với chục chính góc v. Đặt θ = ω + v là góc tọa độ cực. Ta có NP = PF = r; l = 2q = IF; FH = r.cos(θ – ω).
Ta có: NP = IM = IF + FM => r = l + r.cos(θ – ω)
Tiếp tuyến của Parabol: Với các bước tiến hành tương tự như đối với đường elip. Ta có đường thẳng y = mx + c là tiếp tuyến của parabol y2 = 4.q.x khi và chỉ khi c = q/m. Quỹ tích tất cả các điểm mà từ đó kẻ được hai tiếp tuyến với parabol vuông góc với nhau là đường chuẩn.
Phương trình tiếp tuyến của Parabol tại điểm (x2; y2) là: y.y1 = 2q.(x + x1)
Tóm lại: tất cả các đường conic đều có phương trình tọa độ cực dạng:
Và chúng chỉ khác nhau tâm sai:
Đường conic và phương trình đường conic
Khái niệm: Đường conic là hình vẽ được chỉ ra trên mặt phẳng khi nó cắt hoặc tiếp xúc với một hình nón.
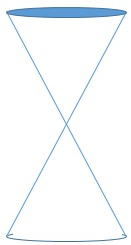 Tùy vào góc độ giao nhau giữa mặt phẳng và hình nón mà nó sẽ tạo ra hình vẽ có thể là hình tròn, hình elip, hyperrbol, đường thẳng, điểm…
Tùy vào góc độ giao nhau giữa mặt phẳng và hình nón mà nó sẽ tạo ra hình vẽ có thể là hình tròn, hình elip, hyperrbol, đường thẳng, điểm…
Để minh họa cho điều này, tìm hiểu một trường hợp là hình elip. Những trường hợp còn lại tiến hành tương tự:
Đề bài: Cho một mặt phẳng cắt nghiêng hình nón với giao tuyến là một vòng K khép kín. Chúng minh hình vẽ K là đường elip.
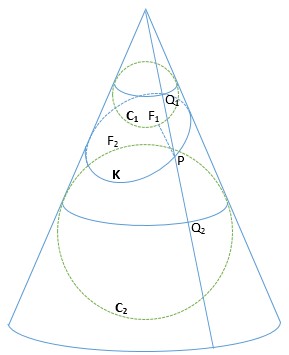 Dựng một hình cầu C1 tiếp xúc trong với hình nón và tiếp xúc trên với mặt phẳng đã cho tại F1. Dựng một hình cầu C2 tiếp xsc trọng với hình nón và tiếp xúc dưới với mặt phẳng đã cho tại F2. Lấy một điểm P trên đường cong K. Vẽ một đường thẳng đi qua đỉnh hình nón và P cắt hình cầu C1 tại Q1 và cắt hình cầu C2 tại Q2. Ta có: PF1 = PQ1 (do đều là tiếp xúc với C1) và PF2 = PQ2 (do đều tiếp xúc với C2), do đó:
Dựng một hình cầu C1 tiếp xúc trong với hình nón và tiếp xúc trên với mặt phẳng đã cho tại F1. Dựng một hình cầu C2 tiếp xsc trọng với hình nón và tiếp xúc dưới với mặt phẳng đã cho tại F2. Lấy một điểm P trên đường cong K. Vẽ một đường thẳng đi qua đỉnh hình nón và P cắt hình cầu C1 tại Q1 và cắt hình cầu C2 tại Q2. Ta có: PF1 = PQ1 (do đều là tiếp xúc với C1) và PF2 = PQ2 (do đều tiếp xúc với C2), do đó:
PF1 + PF2 = PQ1 + PQ2 = Q1Q2
Ta lại có, Q1Q2 độc lập với P. Do đó K là một hình elip với F1 và F2 là những tiêu điểm.
Phương trình tổng quát của các đường conic:
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0
● Đưa về dạng chính tắc:
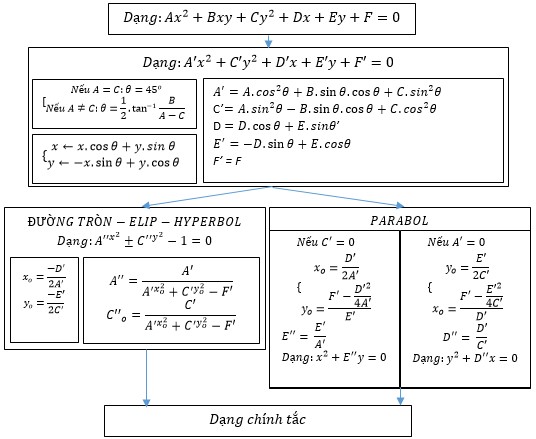
● Nhận dạng các đường conic:
