Công thức lượng giác trong tam giác phẳng

25/11/2022 | Mai Đức Thạch | 322 xem

Tam giác phẳng là hình giới hạn bởi 3 đường thẳng cắt nhau từng đôi một. Trong một tam giác phẳng ABC (ký hiệu ΔABC), ta quy ước ba cạnh AB = c; AC = b và BC = a đo bằng đơn vị độ dài và ba góc $\widehat{BAC}=A$ , $\widehat{ABC}=B$ , $\widehat{ACB}=C$ đo bằng đơn vị góc.

Tam giác phẳng

Định lý cosine

Định lý cosine trong tam giác phẳng Cho AH là đường cao của ΔABC. Sử dụng công thức Pitago ta có:

AC² = AH² + HC² = (AB² – BH²) + (BC – BH)²

= AB² – BH² + BC² + BH² – 2.BC.BH

= AB² + BC² – 2.BC.AB.cos B

Như vậy: b² = a² + c² – 2.a.c.cos B.

Tương tự, ta có các công thức:

a2 = b2 + c2 – 2.b.c.cos A
b2 = a2 + c2 – 2.a.c.cos B
c2 = a2 + b2 – 2.a.b.cos C

Định lý sine

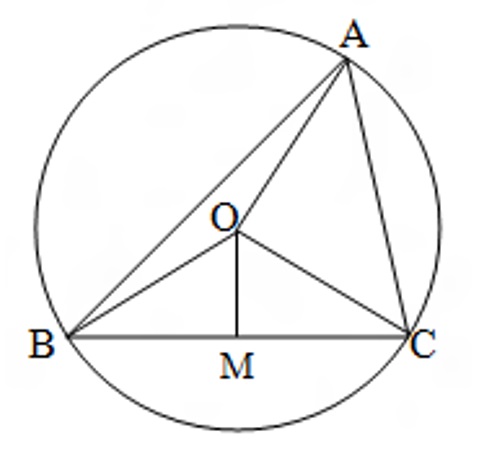Định lý sine trong tam giác phẳng Cho đường tròn (O,R) là đường tròn ngoại tiếp ΔABC; M là trung điểm của BC. Khi đó OM là đường trung trực của BC nên $MB=\frac{BC}{2}=\frac{a}{2}$ .Ta có:

$A=\frac{1}{2}\widehat{BOC}=\widehat{BOM} \Rightarrow sin A=sin \widehat{BOM}=\frac{BM}{OB}=\frac{a}{2R}\Rightarrow \frac{a}{sin A}=2R$

Tương tự ta cũng có:

${\color{Blue} \frac{a}{sin A}= \frac{b}{sin B}= \frac{c}{sin C}=2R}$

Công thức trung tuyến

Công thức trung tuyến trong tam giác phẳng Cho AM là một đường trung tuyến của ΔABC. Áp dụng công thức cosine cho các tam giác ta có:

Trong ΔAMB ta có AM² = AB² + BM² – 2.AB.BM.cos B

Do đó: $m_{a}=c^{2}+\frac{a^2}{4}-a.c.cos B$

Trong tam giác ABC:

$b^2=a^2+c^2-2.a.c.cos B \Leftrightarrow a.c.cos B=\frac{1}{2}(b^2-a^2-c^2)$

Như vậy: $m_a^2=\frac{b^2+c^2}{2}-\frac{a^2}{4}$

Tương tự ta có:

${\color{Blue} m_a^2=\frac{b^2+c^2}{2}-\frac{a^2}{4} }$

${\color{Blue} m_b^2=\frac{a^2+c^2}{2}-\frac{b^2}{4} }$

${\color{Blue} m_c^2=\frac{a^2+b^2}{2}-\frac{c^2}{4} }$

Công thức diện tích

– Gọi h_a, h_b, h_c là độ dài của các đường cao của ΔABC kẻ từ A, B, C. Ta có:

${\color{Blue} S_{\Delta ABC}=\frac{1}{2}.a.h_a=\frac{1}{2}.b.h_b=\frac{1}{2}.c.h_c }$

– Sử dụng định lý sine ta có:

${\color{Blue} S_{\Delta ABC}=\frac{1}{2}.a.b.sin C=\frac{1}{2}.a.c.sin B=\frac{1}{2}.b.c.sin A }$

– Gọi I là tâm đường tròn nội tiếp ΔABC. Đặt r là độ dài bán kính đường tròn nội tiếp ΔABC. Ta có:

$S_{\Delta ABC}=S_{\Delta AIB}+S_{\Delta AIC}+S_{\Delta BIC}=\frac{1}{2}.r.(a+b+c)$

Đặt p là nửa chu vi tam giác ABC: p=(a+b+c)/2. Khi đó:

S_ΔABC= p.r

– Từ công thức cosine ta có:

$cos B=\frac{a^2+c^2-b^2}{2.a.c}$

Ta có:

$sin B=\sqrt{1-cos^{2} B}=\sqrt{1-{\left (\frac{a^2+c^2-b^2}{2.a.c} \right )}^2}=\frac{1}{2.a.c}.\sqrt{(2.a.c)^2-(a^2+c^2-b^2)^2}$
$=\frac{1}{2.a.c}.\sqrt{(2.a.c-a^2-c^2+b^2).(2.a.c+a^2+c^2-b^2)}$
$=\frac{1}{2.a.c}.\sqrt{[b^2-(a-c)^2].[(a+c)^2-b^2]}$
$=\frac{1}{2.a.c}.\sqrt{(b-a+c).(a+b-c).(a+c-b).(a+b+c)}$
$=\frac{1}{2.a.c}.\sqrt{16.p.(p-a).(p-b).(p-c)}=\frac{2}{a.c}.\sqrt{p.(p-a).(p-b).(p-c)}$

Ta lại có: $S_{\Delta ABC}=\frac{1}{2}.a.c.sin B$ nên:

${\color{Blue} S_{\Delta ABC}=\sqrt{p.(p-a).(p-b).(p-c)} }$

Facebook