Công thức lượng giác cho góc

18/10/2020 | Mai Đức Thạch | 15382 xem

Khái niệm chung về công thức lượng giác Trong những phần diễn tả dưới đây, cần đặc biệt lưu ý những trường hợp các góc có số đo là k.90^o (với k thuộc Z).

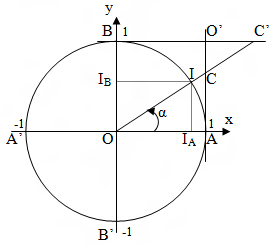
Cho hệ tọa độ Oxy như hình vẽ, một đường tròn (O,1) gọi là đường tròn lượng giác cắt trục Ox tại A(1;0) và A’(-1;0), cắt trục Oy tại B(0;1) và B’(0;-1). Một điểm I(x_I;y_I) nằm trên đường tròn đó. Đặt góc IOA là α. Ta có:

$\sin \alpha =y_{I}=\overline{II_{A}}=\overline{OI_{B}}$

$\cos \alpha =x_{I}=\overline{II_{B}}=\overline{OI_{A}}$

Cho C là giao điểm của đường thẳng qua A song song với trục OI. Ta có:

$\tan \alpha =\overline{AC}$

$\cot \alpha =\overline{BC'}$

Ta đặt:

$\sec \alpha =\frac{1}{\cos \alpha}$ và $\csc \alpha =\frac{1}{\sin \alpha}$

Các hệ thức lượng giác cơ bản

– Từ hình vẽ, ta có: $\Delta OII_{A} \sim \Delta OCA$ nên:

$CA = OA.\frac{II_{A}}{OI_{A}}$ . Do đó: $\tan \alpha =\frac{\sin \alpha}{\cos \alpha}$ . Tương tự: $\cot \alpha =\frac{\cos \alpha}{\sin \alpha}$

– Ta có $\Delta OII_{A}$ vuông tại I_A nên $OI^{2}=OI_{A}^{2}+II_{A}^{2}=1$ . Do đó: sin² α + sin² α = 1

Sử dụng định nghĩa $\sec\alpha$ và $\csc\alpha$ ở trên, thay vào ta có:

1 + tan² α = sec² α
1 + cot² α = csc² α
sec α.csc α = tan α + cot α
sec² α.csc² α = sec² α + csc² α

Hệ thức lượng giác của các cung, góc có liên quan đặc biệt

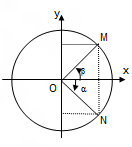
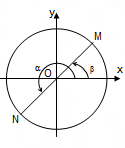
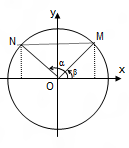
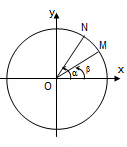
Cung đối nhau (β = -α)	Cung bù nhau (β = 180^o– α)	Cung phụ nhau (β = 90^o – α)	Cung hơn kém 180^o (β = 180^o + α)

sin β = -sin α cos β = cos α tan β = -tan α cot β = -cot α	sin β = sin α cos β = -cos α tan β = -tan α cot β = -cot α	sin β = cos α cos β = sin α tan β = cot α cot β = tan α	sin β = -sin α cos β = -cos α tan β = tan α cot β = cot α

Hệ thức lượng giác của hai góc

Công thức cộng

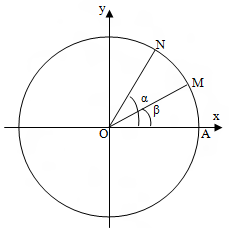Hệ thức lượng giác của hai góc Cho 2 điểm M, N trên đường tròn lượng giác. Đặt $\alpha=\widehat{AON}$ và $\beta=\widehat{AOM}$ . Khi đó, ta có M(cos β; sin β) và N(cos α; sin α).

$\Rightarrow \left\{\begin{matrix} OM=(\cos\beta;\sin\beta)\\ ON=(\cos\alpha;\sin\alpha)\\ OM=ON=OA=1\\ \end{matrix}\right.$

Theo công thức tọa độ ta có:

$\overrightarrow{OM}.\overrightarrow{ON}=\cos\alpha.\cos\beta+\sin\alpha.\sin\beta$

Theo công thức tích vô hướng ta có:

$\overrightarrow{OM}.\overrightarrow{ON}=OM.ON.\cos\widehat{NOM}=\cos(\alpha-\beta)$

Như vậy: cos(α – β) = cos α.cos β + sin α. sin β

Kết hợp sử dụng công thức trên và những hệ thức lượng giác của các cung và góc đặc biệt, biến đồi ta có:

$\sin(\alpha\pm \beta)=\sin\alpha.\cos\beta\pm\cos\alpha.\sin\beta$
$\cos(\alpha\pm \beta)=\cos\alpha.\cos\beta\mp \sin\alpha.\sin\beta$
$\tan(\alpha\pm \beta)=\frac{\tan\alpha\pm\tan\beta}{1\mp \tan\alpha.\tan\beta}$

Công thức biến đổi tổng thành tích

Sử dụng các công thức đã có ở trên biến đổi thành:

$\cos\alpha+\cos\beta=2.\cos\frac{\alpha+\beta}{2}.\cos\frac{\alpha-\beta}{2}$

$\cos\alpha-\cos\beta=-2.\sin\frac{\alpha+\beta}{2}.\sin\frac{\alpha-\beta}{2}$

$\sin\alpha+\sin\beta=2.\sin\frac{\alpha+\beta}{2}.\cos\frac{\alpha-\beta}{2}$

$\sin\alpha-\sin\beta=2.\cos\frac{\alpha+\beta}{2}.\sin\frac{\alpha-\beta}{2}$

Công thức biến đổi tích thành tổng

$\sin\alpha.\sin\beta=-\frac{1}{2}.\left [ \cos(\alpha+\beta)-\cos(\alpha-\beta) \right ]$

$\cos\alpha.\cos\beta=\frac{1}{2}.\left [ \cos(\alpha+\beta)+\cos(\alpha-\beta) \right ]$

$\sin\alpha.\cos\beta=-\frac{1}{2}.\left [ \sin(\alpha+\beta)-\sin(\alpha-\beta) \right ]$

Công thức tan

Đặt $\tan\alpha=T$ và $\tan\frac{\alpha}{2}=t$ ta có:

$\sin\alpha=\frac{T}{\sqrt{1+T^2}}=\frac{2.t}{1+t^2}$

$\cos\alpha=\frac{T}{\sqrt{1-T^2}}=\frac{1-t^2}{1+t^2}$

$\tan\alpha=T=\frac{2.t}{1-t^2}$

Công thức khai triển

$\sin\alpha=\alpha-\frac{\alpha^3}{3!}+\frac{\alpha^5}{5!}-...=\frac{e^{i.\alpha}-e^{-i.\alpha}}{2.i}$

$\cos\alpha=1-\frac{\alpha^2}{2!}+\frac{\alpha^4}{4!}-...=\frac{e^{i.\alpha}+e^{-i.\alpha}}{2}$

Công thức hạ bậc và nâng bậc

$\cos^2\alpha=\frac{1}{2}[\cos(2.\alpha)+1]$

$\sin^2\alpha=\frac{1}{2}[1-\cos(2.\alpha)]$

Trên đây là những công thức lượng giác cho hai góc bất kỳ (lưu ý trong trường hợp k.90^o), khi áp dụng vào tam giác phẳng và tam giác cầu ta có các công thức lượng giác tiếp theo.

Facebook