Tọa độ của hành tinh

Các thông số quỹ đạo hành tinh

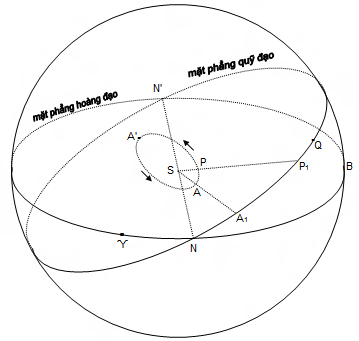
Trong hình vẽ trên, ta biểu diễn một thiên cầu nhật tâm với tâm là Mặt Trời S. Mặt phẳng chứa quỹ đạo hành tinh đi qua Mặt Trời và cắt thiên cầu bởi vòng tròn lớn NQN’ và cắt đường hoàng đạo tại N và N’ – gọi là các điểm nút. Quỹ đạo của hành tinh có A là điểm cận nhật, tia SA cắt vòng tròn lớn NQN’ tại A₁. nếu P là vị trí của hành tinh tại thời điểm t cụ thể, tia SP cắt vòng tròn lớn NQN’ tại P₁. Khi đó:

    (số đo cung A₁P₁)

Hành tinh di chuyển theo chiều từ A tới P như hình vẽ. Khi đó, ta có N gọi là điểm nút lên và N’ gọi là điểm nút xuống.

Góc cầu BNA₁ (ký hiệu i) gọi là độ nghiêng của mặt phẳng quĩ đạo so với đường hoàng đạo.

Số đo cung NA₁ (ký hiệu ω) gọi là đối số của điểm cận nhật.

Cho ϓ là vị trí của điểm xuân phân. Số đo cung ϓN (ký hiệu θ) gọi là kinh độ của điểm nút lên. Tổng số đo của hai cung ϓN và NA₁ (ký hiệu ϖ) gọi là kinh độ của điểm cận nhật. Ta có:

ϖ = θ + ω

Như vậy: θ, i, ϖ, a, e , τ  là các thông số quỹ đạo của hành tinh.

Tổng số đo của cung ϓN và NP₁ (ký hiệu L) gọi là kinh độ thật của hành tinh. Ta có:

L = ϖ + v = θ + ω + v

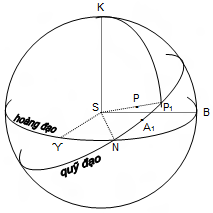
Bây giờ, một vectơ bán kính SA tại thời điểm τ và chuyển động trên quĩ đạo với vận tốc góc trung bình là n. Đến lúc t, vectơ bán kính quét được một góc n.(t – τ) gọi là khoảng cách góc trung bình (ký hiệu M) và ta sẽ biểu diễn điểm đó là Q trên thiên cầu nhật tâm sao đo số đo cung A₁Q = M. Cho l là tổng số đo cung ϓN và NQ, khi đó:

l = θ + ω + n.(t – τ) = ϖ + n.(t – τ)

và l được gọi là kinh độ trung bình của hành tinh.

Cho l = n.t + ε với ε = ϖ + n.τ là kinh độ trung bình khi t = 0 (thời điểm mốc) nên ε được gọi là kinh độ của điểm mốc. Ta có:

M = n.(t – τ) = l – ϖ = n.t – ε – ϖ = E – e.sin E

Tọa độ hành tinh

– Tọa độ nhật tâm hoàng đạo:

Trong hình vẽ trên,  ta có Sϓ, SB, SK là các trục kẻ từ Mặt Trời. Trong đó ϓ là điểm xuân phân, B là điểm trên đường hoàng đạo có kinh độ  hoàng đạo 90^o và K là hoàng cực Bắc.

Cho P là vị trí của hành tinh vào thời điểm t, vectơ bán kính SP = r. Cho P₁ là giao điểm của SP với thiên cầu nhật tâm.

Cho (x₁; y₁; z₁) là tọa độ hình chữ nhật của P lên các trục tọa độ Sϓ, SB và SK. Ta có:

     nên

Tương tự, ta cũng có:

y₁ = r.cos P₁B    và    z₁ = r.cos P₁K

Xét tam giác cầu P₁ϓN có: ϓN = θ, NP₁ = ω + v, P₁Nϓ = 180^o – i. Theo công thức cosine cho tam giác cầu ta có:

cos P₁ϓ = cos θ.cos(ω + v) + sin θ. sin(ω + v).cos i

Khi đó: x₁ = r.[ cos θ.cos(ω + v) + sin θ. sin(ω + v).cos i]

Tưng tự cho các trường hợp còn lại, khi đó ta có:

x₁ = r.[cos θ.cos(ω + v) + sin θ. sin(ω + v).cos i]

y₁ = r.[sin θ.cos(ω + v) + cos θ. sin(ω + v).cos i]

z₁ = r. sin(ω + v).sin i

– Tọa độ nhật tâm xích đạo:

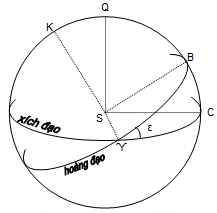
Trong hình vẽ trên, đường tròn ϓC là hình chiếu của đường xích đạo lên thiên cầu. Các tọa độ của hệ tọa độ nhật tâm xích đạo là Sϓ, SC và SQ. Trong đó C là điểm có xích kinh 90^o và Q là bắc cực xích đạo.

Cho (x; y; z) là tọa độ hình chữ nhật của hành tinh khi chiếu lên các trục tọa độ này. Ta có các trục SC và SQ lần lượt nghiêng với trục SB và SK góc ε – là độ nghiêng của đường xích đạo so với đường hoàng đạo.

Chuyển đổi từ tọa độ nhật tâm hoàng đạo sang tọa độ nhật tâm xích đạo:

Từ hình vẽ bên: SP₁ = z₁ ; PP₁ = y₁ ; SP₃ = z; PP₃= y; SP₄= z₁.cos ε; P₃P₄= y₁.sin ε

Từ đó: z = SP₄ + P₃P₄= z₁.cos ε + y₁.sin ε

Ta lại có:

P₁P₄ = P₂P₃ = z₁.sin ε ; PP₂ = y₁.cos ε

 nên: y = PP₂ – P₂P₃ = y₁.cos ε – z₁.sin ε

Từ đó:

x = x₁

y = y₁.cos ε – z₁.sin ε

z = z₁.cos ε + y₁.sin ε

Áp dụng cho Trái Đất (có i = 0^o) có tọa độ nhật tâm xích đạo (x’; y’; z’), ta có:

x’ = r’.cos(θ’ + ω’ + v’) = r’.cos(ϖ’ + v’)

y’ = r’.sin(θ’ + ω’ + v’).cos ε = r’.sin(ϖ’ + v’).cos ε

x’ = r’.sin(θ’ + ω’ + v’).sin ε = r’.sin(ϖ’ + v’).sin ε

– Tọa độ địa tâm xích đạo:

Cho một hệ tọa độ với tâm Trái Đất làm mốc với các trục tọa độ song song với các trục tọa độ gắn với Mặt Trời. Cho (X; Y; Z) là tọa độ của Mặt Trời trong hệ tọa độ đó. Khi đó:

X = -x’ ; Y = -y’ ; Z = -z’

Cho (ξ; η; ζ) là tọa độ của hành tinh vào thời điểm t và (x; y; z) là tọa độ nhật tâm xích đạo của nó. Khi đó ta có:

ξ = X + x; η  = Y + y; ζ = Z + z

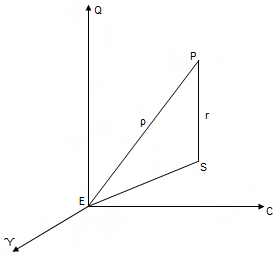
Bây giờ , ta chuyển về thiên cầu địa tâm (tâm E là tâm Trái Đất). Đường thẳng qua E và hành tinh cắt thiên cầu địa tâm tại R. Khoảng cách EP (ký hiệu ρ) là khoảng cách địa tâm của hành tinh vào thời điểm t, ta có:

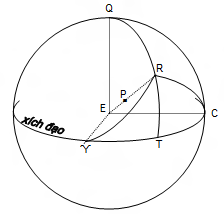
Vẽ kinh tuyến QRT cắt đường xích đạo tại T. Khi đó α, δ là xích kinh và xích vĩ của hành tinh với ϓT = α và TR = δ, đều tính theo đơn vị độ. Ta có:

ξ/ρ = cos PÊT => ξ = ρ.cos Rϓ

Tương tự, ta có: η = ρ.cos RC và ζ = cos RQ

Sử dụng định lý sine trong tam giác cầu RϓT , ta có: cos Rϓ = cos α.cos δ. Do đó:

ξ = ρ.cos α.cos δ     .Tương tự: η = ρ.sin α.cos δ và ζ = ρ.sin δ

Từ đây, ta có tọa độ xích đạo:

     và