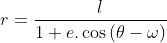Định luật Kepler và Newton về chuyển động của các hành tinh
Hệ Mặt Trời của chúng ta bao gồm 8 hành tinh: Thủy Tinh, Kim Tinh, Trái Đất, Hỏa Tinh, Mộc Tinh, Thổ Tinh, Thiên Vương Tinh, Hải Vương Tinh – quay xung quanh Mặt Trời với quỹ đạo hình elip. Khác với những ngôi sao – những thiên thể ở rất xa Trái Đất nên tọa độ của chúng thay đổi rất chậm, những hành tinh trong hệ Mặt Trời của chúng ta ở những khoảng cách đủ cho chúng ta có thể nhận thấy sự thay đổi vị trí của chúng, chính vì thế, nguồn gốc từ Hy Lạp của hành tinh là: πλάνητεςαστέρες có nghĩa là những ngôi sao lang thang.
Định luật Kepler về chuyển động của hành tinh
Sơ lược tiểu sử Giohanes KeplerKepler sinh năm 1571 trong một gia đình quân nhân. Cậu bé thiếu tháng ấy tưởng đã chết sau khi mới lọt lòng mẹ. Rồi không ngờ cậu lại sống sót. Năm 6 tuổi, cậu lại bị bố mẹ bỏ rơi trong cơn sốt mê sảng vì bệnh đậu mùa. Năm 13 tuổi, cậu lại thoát chết lần thứ ba. Sau khi học xong phổ thông, cậu vào học thần học ở trường đại học, mong trở thành linh mục ở nhà thờ Luthơran. Nhưng rồi ý định ấy bị thay đổi khi ông bộc lộ năng khiếu về toán học. Năm 1594, ông được bổ trợ làm giáo sư toán ở Graz và ông cư trú và xây dựng gia đình ở đó. Bốn năm sau, cả gia đình ông đều phải chạy chốn bởi sự ngược đãi tôn giáo. Ông đến phụ việc cho nhà thiên văn học người Đan Mạch Tikhô Brahê. Lòng say mê thiên văn học của ông bắt đầu từ đây. Trong từng đường đi nước bước, ông không phải là người may mắn. Từ lúc khóc chào đời đến lúc mất, ông phải chiến đấu với bệnh tật, nghịch ảnh và sự ngược đãi. Thậm chí cuối đời, ông đã mất trong mệt mỏi, kiệt sức vì buồn phiền và nghèo túng. Đàn con đông đúc của ông được thừa kế một gia sản sơ sài chỉ gồm 22 đồng floring, 2 chiếc áo sơ mi cũ, 57 cuốn sách và 16 cuốn các bảng phác thảo thiên văn. Anbe Anhxtanh gọi ông là “con người vô song” và đánh giá về ông như sau: “Ông đã sống vào thời đại mà con người chưa có lòng tin. Lòng tin và các quy luật tự nhiên đã khiến ông phải làm việc đơn độc khi không ai ủng hộ và thông hiểu cho mình. Trong mấy chục năm miệt mài gian khổ, cần cù và khó nhọc, ông đã tìm ra bí mật sự chuyển vận của các hành tinh và các định luật toán học của sự chuyển động này”. |
Định luật 1: Mọi hành tinh đều chuyển động quanh Mặt Trời theo các quỹ đạo hình elip với Mặt Trời là một tiêu điểm.
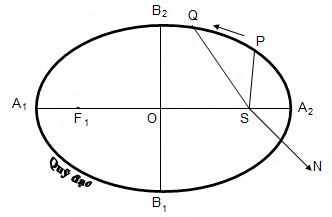
Trong hình vẽ trên ta có: S là Mặt Trời cùng với F1 là 2 tiêu điểm của quỹ đạo hành tinh. O là tâm, A1A2 là trục lớn. Ta có:
• Tại A2, hành tinh gần Mặt Trời nhất, nó được gọi là điểm cận nhật, khoảng cách cận nhật: SA2 = a.(1 – e).
• Tại A1, hành tinh xa Mặt Trời nhất, nó được gọi là điểm viễn nhật, khoảng cách viễn nhật: SA1 = a.(1 + e).
Ta cũng có, bán trục lớn OA2 = a, bán trục nhỏ OB2 = b, tâm sai e = OS/OA2. Ta có: b2 = a2.(1 – e2).
Gọi P là vị trí của hành tinh vào một thời điểm nào đó, ta có r = SP gọi là vectơ bán kính, hay khoảng cách nhật tâm. Cho SN hướng theo một hướng nào đó trên mặt phẳng quỹ đạo hành tinh. Ta đặt góc giữa SN và SP là θ theo chiều chuyển động của hành tinh; cho ω là giá trị của góc θ khi nó đi qua điểm cận nhật. (Đối số của điểm cận nhật). Khi đó:
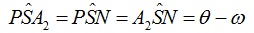
Ta có phương trình cực của quỹ đạo hành tinh:

với l = b2/a = a/(1 – e2)
Thời gian để hành tinh đi hết một vòng trên quỹ đạo của nó (T) gọi là chu kỳ quỹ đạo. Chu kỳ quỹ đạo của Trái Đất là 1 năm (khoảng 365,25 ngày Mặt trời trung bình).
Định luật II: Vectơ bán kính quét những diện tích bằng nhau trong những khoảng thời gian như nhau.
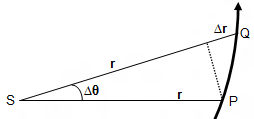
Cho P là vị trí của hành tinh vào thời điểm t, Q là vị trí của nó sau khoảng thời gian ∆t. Khi đó vectơ bán kính SQ tạo với tia SN một góc θ + ∆θ. Ta có góc PSQ nhỏ nên có thể coi PQ như một đoạn thẳng. Khi đó diện tích quét trong thời gian ∆t là S∆PSQ = r.(r + ∆r).sin(∆θ) ≈ r2. ∆θ = const. Ta có:
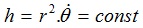
Trong thời gian T, vectơ bán kính quét được một góc là 360o, cho n là tốc độ quét trung bình của vectơ bán kính. Ta có:

Ta lại có Selip = π.a.b, T là chu kỳ nên:
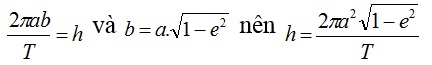

Định luật III: Tỉ số giữa lập phương bán trục chính và bình phương chu kỳ là như nhau cho mọi hành tinh quay quanh Mặt Trời.
Cho a và a1 là bán trục lớn của hai hành tinh và T và T1 là chu kỳ của chúng. Theo định luật III ta có:
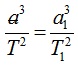
Định luật vạn vật hấp dẫn của Newton và chuyển động của hành tinh
Sơ lược về tiểu sử Isaac NewtonNewton sinh năm 1642 tại Vunxtoc miền Nam nước Anh trong một gia đình điền chủ giàu có. Khi Newton chưa ra đời cha ông đã mất. Hai nă sau mẹ ông lại tái giá. Thủa thơ ấu, Newton sống trong sự chăm sóc, dạy dỗ của ông ngoại và người chú. Khi đi học, Newton vốn yếu ớt, nên thường bị các bạn bắt nạt. Cậu bèn quyết tâm học cho giỏi và quả nhiên sau đó đã trở thành một học sinh suất sắc được bạn bè kính nể. Newton rất say mê với những trò chơi vật lý. Cậu thường tự làm lấy đồ chơi và có những phát minh rất tài tình. Một lần, Newton khoe với các bạn mình rằng nhà mình có một chiếc cối xay thần. Thấy các bạn không tin, cậu dẫn các bạn ra vườn. Ở đó có một chiếc cối xay nhỏ, Kỳ lạ là không cần có sức gió, sức nước hay một lực kéo nào khác mà chiếc cối vẫn quay vù vù và có thể xay được hạt lúa mì thành bột. Các bạn đều thán phục, cho là Newton có phép quỷ thuật. Mãi sau trò quỷ thật đó mới được khám phá. Thì ra Newton đã sử dụng một đàn chuột kéo nhau chạy nhảy theo một hướng làm cối xay quay. Newton có nhiều sáng kiến khác nữa như: chế ra chiếc xe phản lực chạy bằng hơi nước, đồng hồ nước, đồng hồ Mặt trời… Tuy nhỏ tuổi nhưng Newton đã sớm bộc lộ những năng lực phi thường của một nhà phát minh sau này. Năm 1661, khi 19 tuổi, Newton theo học tại trường đại học Kembritgiơ. Tại đây Newton được học cùng với giáo sư Barâu và bắt đầu biết đến hình học Đêcac, số học vô cực của Oalit. Mặc dù đang là sinh viên nhưng Newton đã tìm ra một công thức toán tồn tại mãi đến ngày nay gọi là nhị thức Newton. Cũng từ đó, Newton tiến sâu vào lĩnh vực khoa học và đưa ra những phát minh vĩ đại. Newton mất năm 1727 tại Luân Đôn ở tuổi 85 và không có gia đình. Sự nghiệp khoa học của Newton rất đồ sộ. Ông đã trở thành nhà bác học vĩ đại nhất trong những nhà bác học vĩ đại. – Năm 1665, ở tuổi 23, Newton đưa ra định luật vạn vật hấp dẫn. – Năm 1669, Newton thay thế thầy giáo mình là Barâu, trở thành giáo sư toán của trường Kembritgiơ. Tại đây, Newton đã khám phá ra cấu tạo của ánh sáng trắng. Từ năm 1663-1671, ông giải thích thêm những hiện tượng sinh ra cầu vồng để bổ sung thêm vào môn hình học Đêcac. – Newton còn làm một kính thiên văn để nghiên cứu các vì sao. Trong quyết định nghiên cứu các hiện tượng này, ông đã phát minh ra kính viễn vọng. Kính thiên văn thời này được làm dựa trên những thiết kế của Newton. – Năm 1672, Newton được bầu vào Hội khoa học Hoàng gia, tức viện hàn lân khoa học nước Anh khi đó. – Năm 1704, Newton cho in cuốn "Quang học” mà ông đã viết từ hồi còn ở Kembritgiơ. Bằng trí thông minh tuyệt vời, niềm say mê, sáng tạo không ngừng, Newton đã cống hiến cho nhân loại những phát minh cực kỳ to lớn. Ông mất vào đêm ngày 20, rạng ngày 21/3/1727, tại Luân Đôn. Mộ của ông được đặt tại tu viện Oexmintơn, nơi an nghỉ của các danh nhân nước Anh. Trên bức tường tưởng niệm ông, người ta khắc câu thơ nổi tiếng của Luycrexơ: ”Người đã vượt lên trên tất cả các thiên tài”. Các giai thoại và thí nghiệm nổi tiếng của Newton: – Giai thoại quả táo rụng: Một ần Newton ngồi nghỉ dưới gốc cây táo, chợt một quả táo chín rụng xuống đất, ông thầm hỏi: ”Tại sao quả táo kia không bay lên không trung mà lại rơi xuống đất”. Rõ ràng là Trái Đất đã hút quả táo. Mọi vật đều bị hút vào tâm Trái Đất. Newton đưa ra nhận định: Trong vũ trụ mọi vật tồn tại đều do lực hấp dẫn. Vật có khối lượng càn lớn thì lực hấp dẫn càng cao. Định luật vạn vật hấp dẫn ra đời từ đó. – Phát minh đĩa Newton: trên chiếc đĩa, ông chia ra làm 7 phần, mỗi phần một màu sắc: đỏ- cam- vàng- lục- lam- chàm- tím. Chiếc đĩa này khi quay tít như đĩa hát thì 7 màu sẽ bị hòa lại thành màu trắng. Đó là một thí nghiệm nổi tiếng về cấu tạo của ánh sáng trắng. – Giây phút đãng trí của Newton: vốn là một người yêu động vật, Newton nuôi một con chó và một con mèo. Muốn cho hai con vật đó có thể đi lại tự do trong phòng làm việc của mình, ông cho đục trên tường hai cái lỗ: một to, một nhỏ. Ông đã quên rằng: chỉ cần đục một cái lỗ cũng đủ cho chúng qua lại một cách dễ dàng. |
Định luật vạn vật hấp dẫn: Lực hấp dẫn giữa hai điểm tỉ lệ thuận với tích hai khối lượng và chúng tỉ lệ nghịch với bình phương khoảng cách giữa chúng.

trong đó:
– m và m1: là khối lượng của hai vật.
– r: khoảng cách giữa hai vật.
– G: hằng số hấp dẫn.
Áp dụng vào khảo sát chuyển động của hành tinh:
– Mặt phẳng quỹ đạo chuyển động của hành tinh:

Cho S và P là vị trí của Mặt Trời và hành tinh vào thời điểm t và một hệ tọa độ OXYZ như hình vẽ và chúng có tọa độ lần lượt là S(XS;YS;ZS) và P(XP;YP;ZP).
Theo định luật vạn vật hấp dẫn, hành tinh P chịu tác dụng từ S một lực G.M.m/r2 (với r = SP). Thành phần của lực khi chiếu xuống trục OX là:
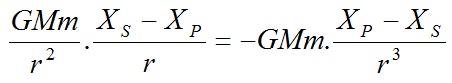
Nếu  là thành phần của gia tốc của P song song với OX, theo định luật II Newton về chuyển động, ta có:
là thành phần của gia tốc của P song song với OX, theo định luật II Newton về chuyển động, ta có:
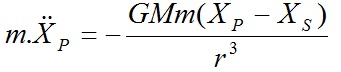 (a)
(a)
Bây giờ, Mặt Trời S chịu tác dụng từ hành tinh P một lực –G.M.m.r2 và khi chiếu lên trục OX là:
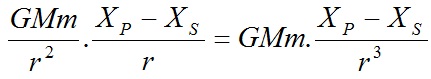
Nếu  là thành phần của gia tốc của S song song với OX, theo định luật II Newton về chuyển động, ta có:
là thành phần của gia tốc của S song song với OX, theo định luật II Newton về chuyển động, ta có:
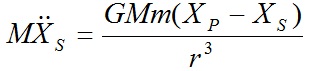 (b)
(b)
Chia (a) với m và (b) với M rồi lấy hiệu của chúng, ta được kết quả:
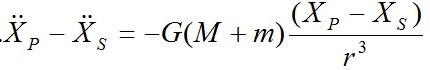 (c)
(c)
Đặt XP – XS = ξ ; YP – YS = η ; ZP – ZS = ζ với (ξ; η; ζ) là tọa độ của hành tinh P với các trục tọa độ gắn với Mặt Trời. Khi đó (c) trở thành:
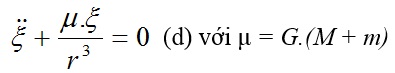
Làm tương tự khi ta chiếu lên các trục OY và OZ, ta có:
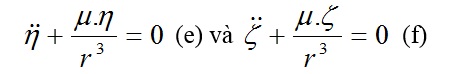
Ba phương trình (d), (e), (f) mô tả chuyển động của P đối với Mặt Trời.
Nhân (e) với ζ và (f) với η rồi lấy hiệu của chúng ta được kết quả:
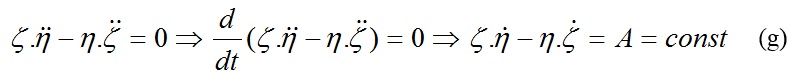
Làm tương tự ta cũng có:
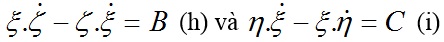
Lần lượt nhân (g), (h), (i) với ξ, η, ζ rồi tính tổng các vế, được kết quả:
A.ξ + B.η + C.ζ = 0
đây là phương trình mặt phẳng quỹ đạo của hành tinh.
– Phương trình chuyển động của hành tinh trên mặt phẳng quỹ đạo của nó:
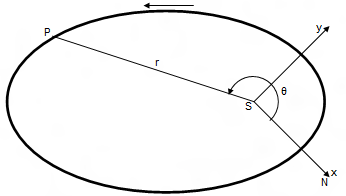
Bây giờ, ta sẽ xét chuyển động của hành tinh với hai trục tọa độ có gốc là Mặt trời và nằm trên mặt phẳng quỹ đạo hành tinh. Đó là hệ trục tọa độ Sxy như hình vẽ. Ở đây, SN là trục x, trục y vuông góc với trục x theo chiều chuyển động của hành tinh. Ta có phương trình chuyển động của hành tinh tương tự như đã được phân tích ở phần trên:
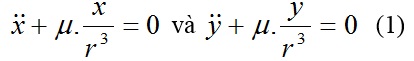
Công thức chuyển đổi từ tọa độ hình chữ nhật sang tọa độ cực, ta có:
x = r.cos θ và y = r.sin θ (2)
Cho α và β là thành phần gia tốc của P khi chiếu lên các trục tọa độ, ta có:
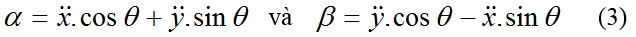
Từ phương trình đầu tiên của (2), ta lấy vi phân:
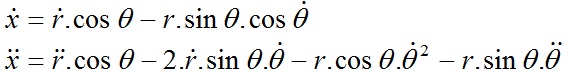
Tương tự cho phương trình thứ hai:
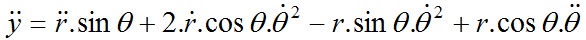
Thay 2 phương trình ẍ và ӱ có ở trên vào phương trình đầu tiên của (3), ta được:
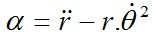
Thay 2 phương trình của (1) và phương trình đầu tiên của (3), rồi thay x,y từ hai phương trình của (2) và kết quả thu được. Rút gọn lại ta được:

Như vậy:
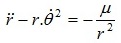 (4).
(4).
Tương tự ta cũng có: 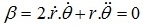
Mà:
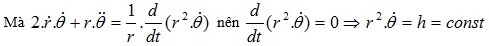
Đặt u = 1/r, khi đó phương trình h trở thành: 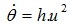 (5)
(5)
Ta lại có:
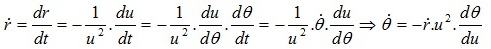
thế vào phương trình trên ta có:
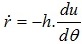
Ta lại có:
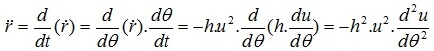 (6)
(6)
Bình phương 2 về của (5) rồi nhân với r ta được: 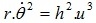 (7)
(7)
Thế (6) và (7) vào (4) ta được:

|
Giải phương trình vi phân:
Đặt
Đặt thay trở lại công thức (1) ta có:
Ta lại có: mà
Đặt A = a + b và B = i.(a – b) ta có:
Từ công thức (2) ta có:
Đặt
Mà r = 1/u nên:
Đặt
(Đây là phương trình tọa độ cực của 1 đường conic) |
Áp dụng cho các hành tinh có e<1 => đó là phương trình của một đường elip.
– Vận tốc của hành tinh trên quỹ đạo của nó:
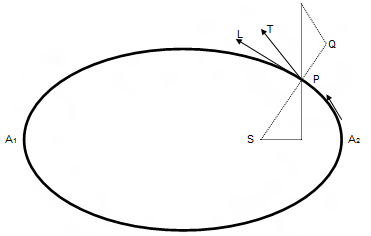
Trong hình vẽ bên V được biểu diễn bởi PT (tiếp tuyến của elip), r được biểu diễn bởi PQ và 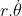 được biểu diễn bởi PL (vuông góc với PQ). Khi đó:
được biểu diễn bởi PL (vuông góc với PQ). Khi đó:
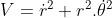
với:
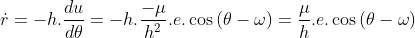
Từ  ta có:
ta có:
![r.\dot{\theta}=h.u=\frac{\mu}{h}.[1+e.\cos(\theta-\omega)]](/images/1/images/chuyen-dong-cua-hanh-tinh/04.gif)
Từ đó:
![V^{2}=\frac{\mu}{h^{2}}.[2+2.e.\cos(\theta-\omega)-(1-e^{2})]](/images/1/images/chuyen-dong-cua-hanh-tinh/05.gif)
Mà  và u=1/r, ta có:
và u=1/r, ta có:
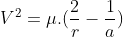
Hành tinh di chuyển nhanh nhất khi r nhỏ nhất (tại vị trí hành tinh qua điểm cận nhật):
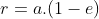 và
và 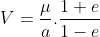
Hành tinh di chuyển chậm nhất khi r lớn nhất (tại vị trí hành tinh qua điểm viễn nhật):
 và
và 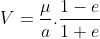
Các công thức cơ bản
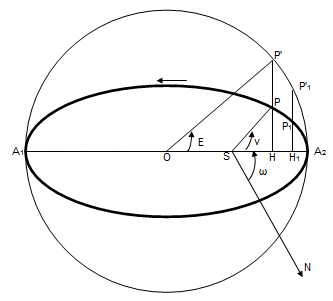
– Khoảng cách góc thật và khoảng cách góc lệch tâm:
Khoảng cách góc thật (v) là khoảng cách góc từ vị trí của hành tinh vào một thời điểm đến điểm cận nhật nhìn từ Mặt Trời theo chiều chuyển động của hành tinh. Ta có: 
Khoảng cách góc lệch tâm (E) là khoảng cách góc của hành tinh khi chiếu lên đường tròn đến điểm cận nhật nhìn từ tâm quỹ đạo theo chiều chuyển động của hành tinh. Ta có: 
Ta có công thức liên hệ giữa khoảng cách góc thật và khoảng cách góc lệch tâm:

– Phương trình Kepler:
Ta gọi τ là thời điểm hành tinh đi qua điểm cận nhật và T là chu kỳ quỹ đạo. Vào thời điểm t, hành tinh đang ở vị trí P. Trong khoảng thời gian (t – τ), vectơ bán kính di chuyển từ SA2 tới SP và quét được diện tích SPA2. Theo định luật II Kepler:
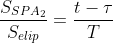 . Do đó:
. Do đó: 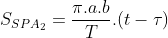
Từ định nghĩa góc chuyển động trung bình n. Góc n.(t – τ) biểu thị cho góc tại thời điểm (t – τ) bởi một vectơ bán kính quanh S với hằng số vận tốc góc n. Đặt M = n.(t – τ) gọi là khoảng cách góc trung bình. Khi đó:
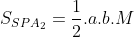
Ta lại có: 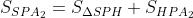 . Trong đó:
. Trong đó:
* 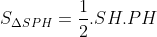 với
với 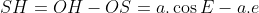 và
và  nên:
nên: 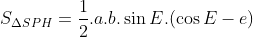
* Ta vẽ các đường thẳng vuông góc với A1A2 như P1H1. Ta có: P1H1 = b.P’1H/a. Tính tổng độ dài tất cả các đoạn thẳng như thế ta được:
![S_{HPA_{2}}=\frac{b}{a}.S_{HP'A_{2}}=\frac{b}{a}.(S_{OP'A_{2}}-S_{\Delta OP'H})=\frac{b}{a}.[\frac{1}{2}.a^{2}.E-\frac{1}{2}.a^{2}.\sin{E}.\cos{E}]=\frac{1}{2}.a.b.(E-\sin{E}.\cos{E})](/images/1/images/chuyen-dong-cua-hanh-tinh/23.gif)
Như vậy: 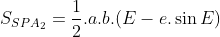
Từ đó, ta có:
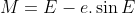
– Phương trình trung tâm:
* Giải phương trình Kepler M = E – e.sin E:
Ta có E = M + e.sin E
Cho E1 = M ta lần lượt tính E2 = M + e.sin E ; E3 = M + e.sin E2 ;
E3 = M + e.sin(M + e.sin M) = M + e.sin M.cos(e.sin M) + e.cos M.sin(e.sin M)
với E là một số nhỏ, ta có: E3 = M + e.sin M + e.cos M.e.sin M = e.sin M + e2.sin(2.M)/2
Làm tiếp khai triển như thế ta được:
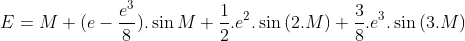 (1)
(1)
* Giải phương trình liên hệ giữa khoảng cách góc thật và khoảng cách góc lệch tâm:
Đặt 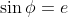 với
với 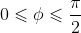 ta có:
ta có: 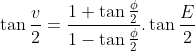
Đặt 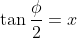 ta có
ta có 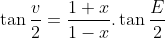
Từ 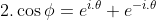 và
và 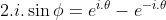 , ta có thể viết:
, ta có thể viết:
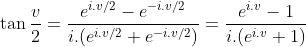
Làm tương tự với tan(E/2) và ghép lại ta được:
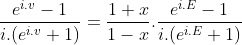
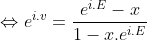
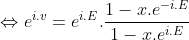
Logarit 2 vế: 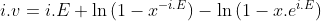
Bây giờ với 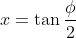 và
và 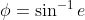 với x<1 và e<1, ta có:
với x<1 và e<1, ta có:

với 
Khi đó: 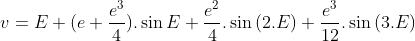 (2)
(2)
* Phương trình trong tâm:
Từ (1) ta có:
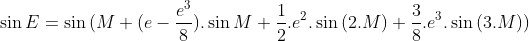
Với độ chính xác giới hạn trong e2 nên công thức trên trở thành:
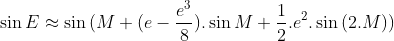
![=\sin{M}.\cos{[e.\sin{M}+\frac{e^{2}}{2}.\sin{(2.M)}]}+\cos{M}.\sin{[e.\sin{M}+\frac{e^{2}}{2}.\sin{(2.M)}]}](/images/1/images/chuyen-dong-cua-hanh-tinh/44.gif)
![\approx \sin{M}.(1-\frac{e^{2}}{2}.\sin{(2.M)})+\cos{M}.\sin{[e.\sin{M}+\frac{e^{2}}{2}.\sin{(2.M)}]}](/images/1/images/chuyen-dong-cua-hanh-tinh/45.gif)
![\approx \sin{M}+\frac{e}{2}.\sin{(2.M)}+\frac{e^{2}}{2}.[\sin{(2.M)}.\cos{M}-\sin{(3.M)}]](/images/1/images/chuyen-dong-cua-hanh-tinh/46.gif)
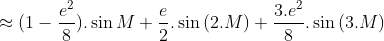
Trong giới hạn cần thiết khai triển tương tự ta cũng có:
sin(2.E) = sin(2.M) + e.[sin(3.M)-sinM] và sin(3.E) = sin(3.M)
Thay sin E, sin(2.E), sin(3.E) khai triển ở trên vào công thức (2) ta được:
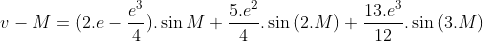

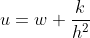 (2), thay vào phương trình ta có:
(2), thay vào phương trình ta có: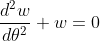 (1)
(1)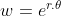 có các khai triển:
có các khai triển: 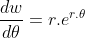 và
và 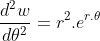
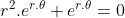

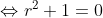
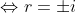
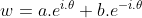
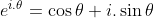 thay trở lại công thức trên ta có:
thay trở lại công thức trên ta có:
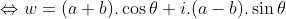
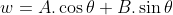
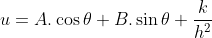
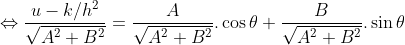
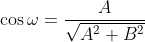 thì
thì  ta có:
ta có: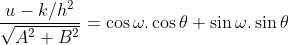
 và
và  ta có:
ta có: